우리는 일상 생활에서 두 변수들 간의 관계에 대한 정보가 궁금할 때가 많다. 예를들어 온도와 아이스크림 판매량 간의 관계라던가, 분기 결산과 연말 결산의 관계가 궁금할 수 있다. 물론 경험에서 얻을 수 있는 정보로 변수들 간의 관계를 추론해볼 수 있지만, mathematical equation을 모델링할 수 있다면 정확한 관계를 파악할 수 있을 것이다.
1. $Y=f(X)+\epsilon$
두 변수 X와 Y간의 관계에 대하여 다음과 같은 functional equation을 가정해보자.
\[Y=f(X)\]하지만 이러한 모형은 현실과는 잘 맞지 않는 모형인데, 다음의 경우를 생각해보면 알 수 있다. X축은 Midyear evaluation이고, Y축은 year-end evaluation이다.
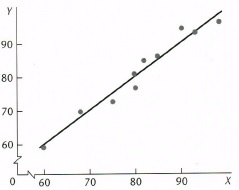
이 경우 실제 현실에서의 데이터는 하나의 직선 함수로 나타나는 것이 아닌, 그 함수를 중심으로 $\textbf{error}$가 존재한다는 것을 알 수 있다. 즉, $Y=f(X)$으로 모델을 가정하는 것은 변수들간의 관계를 잘못 가정한 것이라 볼 수 있다. 따라서 우리는 오차항을 고려하여, 다음의 모델을 가정하게 된다.
\[Y=f(X)+\epsilon\]
2. $Y=\beta_{0}+\beta_{1}X+\epsilon$
앞서 우리는 $y$와 $x$간의 관계를 $Y=f(X)+\epsilon$로 정의하였다. 이제 모델을 조금 더 구체화시켜보자. 간단한 설명을 위하여 하나의 독립변수만 존재하는 Simple Linear Regression을 생각해보자. $n$개의 observation이 존재한다면, 우리는 다음과 같은 회귀 모형을 가정할 수 있다.
\(Y_{i}=\beta_{0}+\beta_{1}X_{i}+\epsilon_{i}\;\;;i=1,\cdots,n\)
$\beta$의 평균과 분산에 대한 가정
통상적으로 Linear Regression이라 함은, fixed effect linear model을 의미한다. Fixed effect model에서 $\beta$는 분포를 갖지 않는 상수로 가정된다. 따라서 이 글에서 $\beta$의 평균과 분산은 다음과 같다.
$E[\beta]=\beta$
$Var[\beta]=0$
$\epsilon$의 평균과 분산에 대한 가정
$E[\epsilon]=0$
$Var[\epsilon]=\sigma^2$
중요한 것은 아직 우리는 오차 $\epsilon$에 대한 분포를 가정하지 않았다는 것이다. 이 이야기에 대한 후반부에 다시 설명하도록 하겠다.
Y의 평균과 분산
드디어 위의 결과들로부터, 다음의 결과를 도출해낼 수 있다.
$E[Y]=\beta_{0}+\beta_{1}X$
$Var[Y]=\sigma^2$
3. Key assumptions
우리는 앞선 내용에서 기본적인 Simple Linear Regression 모형을 생각해보았다. Linear Regression에서 중요한 4가지 가정사항들을 정리해보면 다음과 같다.
a. Linearity
b. Constant Variance
c. Independence of errors
d. Normality of errors($\epsilon$) : for inferences
4가지 가정 사항들에 대하여 차근차근 하나씩 살펴보도록 하겠다.
a. Linearity
“$E[Y]=\mu$ 에 대해 선형 모형을 가정한다.”
우리는 앞서 다음과 같이 모델을 가정하였다.
\[E[Y]=\beta_{0}+\beta_{1}X\]우리는 위와 같이 $E[Y]$를 선형모형으로 가정한 것이다. 즉, Linear Regression에서는 $E[Y]$의 linearity를 가정한다.
그렇다면 $E[Y]$를 선형모형으로 가정하는 것이 무조건 타당한 것이라고 할 수 있을까? 그것은 아니다. $\mu = E[Y]$를 linear combination으로 나타내지 않고 다른 함수를 사용하여 모델을 나타내는 경우도 많다.
자세한 이야기는 GLM(Generalized Linear Model)을 살펴볼 때 말하도록 하겠지만, Linear Regression의 경우 link function이 $g(\mu)=\mu=X^T\beta$로써 link function이 identity function이다. 즉, $E[Y]$에 대한 선형모형을 가정한다.
하지만 Logistic Regression의 경우 link function $g(\mu)={\mu \over 1-\mu}=X^T\beta$로 $E[Y]$에 대해 linearity를 가정하지 않는다는 것을 알 수 있다.
b. Constant Variance
“$Y$의 분산, 곧 $\epsilon$의 분산은 일정하다”
수식으로 나타낸다면 다음과 같다.
$Var[Y] = Var[\epsilon] = \sigma^2$
c. Independence of errors
“오차항은 서로 독립이다”
$\epsilon_{i} \overset{\text{indep}}{\sim} \cdot,\;\;i=1,2,…,n$
d. Normality of errors(Inferences를 위한 추가적인 가정 사항)
”$\epsilon$은 정규분포를 따른다”
$\epsilon_{i} \overset{\text{iid}}{\sim} N(0, \sigma^2),\;\;i=1,2,…,n$
마지막 가정 d는 LSE(Least Squared Estimation) 자체를 구할 때에는 필요하지 않은 가정이다. 역사적으로 살펴보았을 때에도 Gauss가 LSE를 발견한 이후, 세월이 많이 지난 뒤에 모수에 대한 C.I.(Confidence Interval)을 구하거나 가설검정을 하기 위하여 $\epsilon$에 대한 분포를 가정하기 시작했다. 따라서 이어서 살펴볼 Least Squared Estimation을 통한 $\beta$의 Estimation에는 가정 d.는 필요하지 않다.
4. LSE : Least Squared Method
LSE의 컨셉은 실제 값과 예측하는 값의 차이($\epsilon$)를 가장 작게 만드는 $\beta$를 추정하여, 실제 값과 모델이 예측하는 값의 차이를 최대한 줄이는 것이다.
\[Q(\beta_0,\beta_1) = \sum\limits_{n=1}^{n} \epsilon^{2} = \sum\limits_{n=1}^{n} (y_i-\beta_0-\beta_1x_i)^{2}\]위의 식을 가장 최소화하는 $\beta_0, \beta_1$을 각각 $\hat{\beta_{0LSE}}$, $\hat{\beta_{1LSE}}$라고 하자.
\[(\hat{\beta_0}_{LSE}, \hat{\beta_1}_{LSE}) = argmin_{(\beta_0,\beta_1)}Q(\beta_0,\beta_1)\]$Q(\beta_0,\beta_1)$를 최소화하는 $\beta_0,\beta_1$의 값들을 구할 수 있고, 그 값들이 바로 $\hat{\beta_{0LSE}}$, $\hat{\beta_{1LSE}}$가 된다.
5. MLE : Maximum Likelihood Estimator
우리는 앞서 회귀 모형의 모수를 LSE로 추정해 보았다. 한 가지 모수를 추정하는 방법은 무한히 많이 존재할 수 있는데, 이번에는 MLE를 사용하여 $\beta$를 추정해보자.
MLE를 구하기 위해서는 Likelihood를 구해야하고, Likelihood를 구하기 위해서는 $\epsilon$의 분포를 가정해야 한다.(LSE에서는 분포에 대한 가정 없이도, LSE를 구할 수 있었다.)
$\epsilon$의 분포를 다음과 같이 가정해보자.
\[\epsilon_{i} \overset{iid}{\sim} N(0,\sigma^2)\]이 때 Y의 분포는 다음과 같다.
\[Y_{i} \overset{iid}{\sim} N(\mu,\sigma^2)\]Likelihood는 다음과 같이 구할 수 있다.
\[\begin{aligned} L(\mu, \sigma^2|y) &= \prod_{i=1}^{n} f_{\mu}(y_i)\\ &=\prod_{i=1}^{n} {1\over{\sqrt{2\sigma^2}}}\exp[-{1\over{2\sigma^2}}(y_{i}-\mu)^2] \end{aligned}\]이 Likelihood를 Maximize하는 $\beta_0, \beta_1$이 바로 MLE(Maximum Likelihood Estimator)이다.
\[(\hat{\beta_0}_{mle}, \hat{\beta_1}_{mle}) = argmax_{(\beta_0,\beta_1)}L(\mu, \sigma^2|y)\]
6. LSE와 MLE의 관계
이제 우리는 우리가 가정한 모형에서 LSE와 MSE를 구할 수 있다. 모수 $\beta_0, \beta_1$에 대해 LSE와 MSE를 각각 구해보면 다음과 같은 관계가 성립한다는 것을 알 수 있다.
\[\begin{aligned} \hat{\beta_0}_{LSE} &= \hat{\beta_0}_{mle}\\ \hat{\beta_1}_{LSE} &= \hat{\beta_1}_{mle} \end{aligned}\]즉, $\beta$의 LSE와 MSE는 같다. 반면 $\sigma^2$의 경우, LSE와 MSE가 다음과 같은 관계를 가진다.
\[\hat{\sigma^2}_{LSE} = {n \over (n-2)}\hat{\sigma^2}_{mle}\]즉, $\sigma^2$의 LSE와 MSE는 다르다. \(\hat{\sigma^2}_{LSE} \neq \hat{\sigma^2}_{mle}\)
참고로 덧붙이면, $\sigma^2$의 mle는 biased estimator이다. 반면, $\sigma^2$의 LSE는 unbiased estimator이다.
\[\begin{aligned} E[\hat{\sigma^2}_{mle}] &\neq \sigma^2\\ E[\hat{\sigma^2}_{LSE}] &= \sigma^2 \end{aligned}\]Reference
Yongho Jeon(2016), REGRRESSION ANALYSIS : Linear Regression with One Predictor Variable, Yonsei University, 1-31