Related Post
우선, Hierarchical Linear Model을 살펴보기 위하여 linear regression의 간단한 example부터 이야기를 시작해보도록 하자.
1. Simple Linear Regression
이 예제는 Hierarchical linear models(2002) 책 초반부에 나오는 유명한 예제다.
한 학교에서 학생들의 SES(Socioeconomic status) score를 $X_i$, 수학 성적을 $Y_i$라고 하자.(SES score는 ‘해당 학생(혹은 부모님)의 사회경제학적 지위’를 점수로 변환한 것이라고 생각하면 된다.)이 때 다음과 같은 회귀 모형을 만들 수 있다.
\[Y_i = \beta_0 + \beta_1 X_i + \epsilon_i\]이 때 $\beta_0$는 SES가 0점인 학생의 수학 성적의 기대값이다. 그리고, $\beta_1$은 SES가 한 단위 증가할 때의 수학 성적 변화의 기대값이다. Error term인 $\epsilon_i$는 i 번째 사람의 unique effect라고 할 수 있다. 일반적인 회귀 모형에서는 $\epsilon_i$의 분포에 대하여 다음과 같이 가정한다.
\[\epsilon_i \sim N(0, \sigma^2)\]
2. Simple Linear Regression: Centering
이 때 intercept $\beta_0$가 의미를 가질 수 있도록 만들어 주기 위하여, 우리는 X를 ‘centering’을 통해 scaling해줄 수 있다.
\[Y_i = \beta_{0} + \beta_{1} (X_i-\overline{X}) + \epsilon_{i}\]즉 $X_i$대신 $X_i-\overline{X}$를 사용하는 것이다. 이 때 slope $\beta_{1}$에 대한 해석은 바뀌지 않지만, intercept $\beta_{0}$에 대한 해석이 바뀌게 된다. ‘centering’후 $\beta_{0}$는 ‘평균 수학 성적’으로 해석할 수 있게 된다.
위와 같은 회귀 모형을 두 학교 (School A, School B)에 적용한다면, 각각 하나의 회귀 모형을 얻을 수 있다.
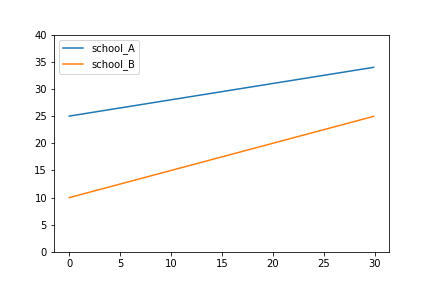
만약 두 학교에 학생들이 random하게 배정된 것이라면, 우리는 A학교의 평균 수학점수가 B학교의 평균 수학점수보다 높다고 할 수 있다.($\because \beta_{0A} > \beta_{0B}$) 마찬가지로, $\beta_{1A} < \beta_{1B}$에 대한 해석도 가능하다.
하지만 학생들이 두 학교에 random하게 배정되었다고 보는 것은 우리의 모델을 간단하게 하기 위한 것일 뿐, 현실적이지 않은 가정이다.
3. Hierarchical Model
이제는 모든 학교(J개의 학교, J is large enough)에 대하여 SES-수학 성적의 관계에 대해 생각해보자. Simplicity를 위하여 각 학교의 분산은 $\sigma^2$로 같다고 하자.(homogeneous variance across schools)
\[\begin{align} Y_{ij} &= \beta_{0j} + \beta_{1j} (X_{ij}-\overline{X}_{\cdot j}) + \epsilon_{ij},\;\; \;\epsilon_{ij} \sim N(0, \sigma^2) \end{align}\]fixed model에서는 $\beta_{0j}$와 $\beta_{1j}$에 대하여 fixed라고 가정한다. 하지만 Hierarchical model에서는 다르다. 두 모수 $\beta_{0j}$와 $\beta_{1j}$에 대하여 bivariate normal distribution을 가정해보자.
\[\begin{align*} \begin{bmatrix} \beta_{0j} \\ \beta_{1j} \end{bmatrix} \sim N \begin{pmatrix} \begin{bmatrix} \gamma_0 \\ \gamma_1 \end{bmatrix} , \begin{bmatrix} \tau_{00} & \tau_{01} \\ \tau_{01} & \tau_{11} \end{bmatrix} \end{pmatrix} \end{align*}\]참고로 $\rho(\beta_{0j},\beta_{1j})$는 다음과 같이 구할 수 있다.
\[\rho(\beta_{0j},\beta_{1j}) = \tau_{01}/(\tau_{00}\tau_{11})^{1/2}\]현실에서 우리는 $\beta_{0j}, \beta_{1j}$는 모르는 경우가 대부분이며, $\gamma_0,\gamma_1,\tau_{01},\tau_{00},\tau_{11}$에 대해서도 역시 알 수 없는 경우가 대부분이다. 즉, 이러한 모수들을 추정해야하는 것이다.
만약 학교 간 특성에 차이가 존재한다면(혹은 학생들이 random하게 배정된 것이 아니라면), 이 특성을 반영해줄 수 있는 모델을 만들어야 한다. 이러한 특성을 반영해줄 수 있는 Indicator variable $W_j$를 사용할 수 있다. 다음과 같이 $W_j$를 가정해보자.
\[\begin{align*} W_j = \begin{cases} 1 \;\;\; if\;School\;j\;is\;Mission\;school\\ \\ 0 \;\;\;\; if\;School\;j\;is\;Public\;school\\ \end{cases} \end{align*}\]그리고 다음과 같이 두 regression equations를 가정해보자.
\[\begin{align} \beta_{0j} &= \gamma_{00}+\gamma_{01}W_j+u_{0j}\\ \beta_{1j} &= \gamma_{10}+\gamma_{11}W_j+u_{1j} \end{align}\] \[where \; \begin{align*} \begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim \begin{pmatrix} \begin{bmatrix} 0 \\ 0 \end{bmatrix} , \begin{bmatrix} \tau_{00} & \tau_{01} \\ \tau_{01} & \tau_{11} \end{bmatrix} \end{pmatrix} \end{align*}\]이 $\tau_{00}, \tau_{01}, \tau_{11}$를 Conditional variance-covariance component, 혹은 Residual variance-covariance component 라고 한다.즉, $W_j$를 Controlling한 뒤의 $\beta_{0j}$와 $\beta_{1j}$의 variability를 나타낸다. (참고로 Random effect model에서 random effect의 분산을 Variance component 라고 한다.)
$(\beta_0, \beta_1)$가 직접적으로 관측되지 않으므로, 위의 두 regression equations의 parameters를 직접적으로는 추정할 수 없다. 그러나 추정을 위해 필요한 정보는 data에 포함되어 있다.
식 (1), (2), (3)을 통하여 다음 single prediction equation을 유도할 수 있다.
\[\begin{align*} Y_{ij} &= \beta_{0j} + \beta_{1j} (X_{ij}-\overline{X}_{\cdot j}) + \epsilon_{ij}\\ &= (\gamma_{00}+\gamma_{01}W_j+u_{0j}) + (\gamma_{10}+\gamma_{11}W_j+u_{1j})(X_{ij}-\overline{X}_{\cdot j})+\epsilon_{ij}\\ &= \gamma_{00}+\gamma_{01}W_j+\gamma_{10}(X_{ij}-\overline{X}_{\cdot j})+\gamma_{11}W_j(X_{ij}-\overline{X}_{\cdot j})+u_{0j}+u_{1j}(X_{ij}-\overline{X}_{\cdot j})+\epsilon_{ij\cdot} \end{align*} \\\]마침내 기본적인 Hierarchical linear model을 구했다. 이 모델에서 Fixed Effect는 $\gamma_{00}, \gamma_{10}$이며, Random Effect는 $\gamma_{01}, \gamma_{11}$이다.
4. Linear Regression(OLS) & Hierarchical Model
위 모델은 OLS(Ordinary Least Squares) linear regression model과는 분명하게 다르다.
OLS는 OLS에 기반한 Estimation과 Inference(가설검정 등)를 위하여 random errors에 대하여 independent와 normally distributed, constant variance를 가정한다.
반면 우리가 가정한 Hierarchical linear model에서의 random error
\[\delta_{ij} = (u_{0j}+u_{1j}(X_{ij}-\overline{X}_{\cdot j})+\epsilon_{ij\cdot})\]의 경우, 그렇지 않다.
dependent
우선, $\delta_{ij}$는 Independent하지 않다.
예를들어, $u_{0j}$와 $u_{1j}$는 j번째 학교의 모든 학생들에대하여 같은 값을 가진다. 따라서 독립이라고 볼 수 없다.
unequal variances
$\delta_{ij}$의 분산은 일정하지 않다.
$\delta_{ij}$의 분산은 $u_{0j}$와 $u_{1j}$에 의존하는 식으로 나타낼 수 있다. 하지만 $u_{0j}$와 $u_{1j}$는 학교마다 달라질 것이다. 따라서 Constant Variance라고 볼 수 없다.
즉, 오차항에 대하여 independence와 equal variance를 가정하는 일반적인 linear regression으로는 이러한 특징의 자료를 분석하는 것이 부적절하다고 할 수 있다.
Reference
Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (Vol. 1). Sage. 16-22