알고리즘의 복잡도(Complexity of Algorithm)

어떠한 알고리즘을 나의 노트북과 슈퍼컴퓨터에서 각각 돌린다면 task 수행 가능의 정도나, 알고리즘의 속도에 있어 분명히 차이가 날 수밖에 없다. 어떤 알고리즘에 대한 평가, 혹은 비교를 할 때 같은 환경에서 이루어지지 않는다면 이는 공정한 평가가 될 수 없다.

이러한 문제를 해결하기 위해 컴퓨터의 성능과는 독립적으로 알고리즘의 복잡한 정도를 나타낼 수 있는 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)라는 척도를 사용한다.

우선 시간 복잡도는 입력 데이터의 크기(n)와 알고리즘의 소요 시간의 관계다. 즉, 데이터의 크기가 커지면 어떠한 관계로 소요 시간이 커지는가를 나타낸 것이다.

반면 공간 복잡도의 경우 입력 데이터의 크기가 주어졌을 때 알고리즘의 소요 메모리 공간의 관계다. 즉, 데이터의 크기가 커지면 어떠한 관계로 소요 메모리 공간이 커지는가를 나타낸 것이다.



Big O notation

가장 많이 사용하는 notation은 Big O notation이다. 이 Notation을 고안해낸 독일의 수학자 Edmund Landau의 이름을 따서 Laudau’s symbol이라고도 부르기도 한다.

Big O notation에서 대문자 O 를 사용하는 것은 함수가 증가(혹은 감소)하는 rate을 뜻하는 Order 에서 따온 것이라고 한다.

Big O notation은 complexity theory, computer science, mathematics에서 어떠한 함수의 asymptotic behavior를 나타낼 때 사용되는 개념이다. 기본적으로 이 노테이션은 이 함수가 얼마나 빠르게 증가 혹은 감소하는지를 나타낸다.


Definition of function O

some subset of real number에서 정의된 두 함수 $f(x)$와 $g(x)$를 가정해보자. Big O function은 다음과 같이 정의된다.


\[\begin{align*} f(x) = O(g(x))\;\;for\;x \rightarrow \infty\\\\ \text{if and only if there exist constants N, C such that}\\\\ |{f(x)}| \leq C |g(x)|\;\;\text{for all x >N} \end{align*}\]


즉, 상수 N이상의 support에서 $C \vert g(x) \vert \geq f(x)$ 가 되도록 하는 constant C가 존재한다면, 우리는 $f(x) = O(g(x))$라고 한다.

다음 그림을 살펴보자.



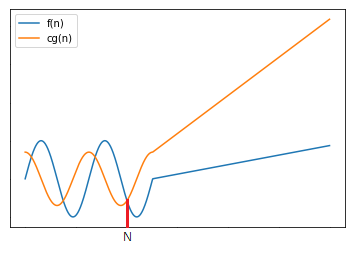
나의 알고리즘을 $f(n)$이라고 하자. 위 그림을 만족할 경우 $f(n)=O(g(n))$, 즉 나의 알고리즘의 계산복잡도 $g(n)$을 가진다고 할 수 있다. 이 때 g(n)을 f(n)의 점근 상한(Asymptotic upper bound) 이라고 한다.

이는 나의 알고리즘 $f(n)$이 계산복잡도 g(n)을 가진다면, 즉 $f(n) = O(g(n))$이라면,

$f(n)$의 계산복잡도는 최악의 경우에도 $g(n)$보다 작거나 같다는 의미를 가진다.

참고로 다음은 알고리즘을 공부하다 보면 많이 마주치게 되는 계산복잡도의 이름들을 정리한 것이다. n이 증가함에 따라 복잡도가 더 느리게 증가하는 순으로(위에서 아래로) 정리되어 있다.

notation
name
$O(1)$
constant
$O(log(n))$
logarithmic
$O({(log(n))}^c$)
polylogarithmic
$O(n)$
linear
$O(n^2)$
quadratic
$O(n^c)$
polynomial
$O(c^n)$
exponential

$\;\text{for some constant c}$



Another notation

가장 많이 사용하는 notation은 Big O notation이지만, 이외에도 다른 notation들을 사용하기도 한다.

notation
name
$f(n) = \omega(g(n)) $
$f \gt g$
$f(n) = \Omega(g(n)) $
$f \geq g$
$f(n) = \Theta(g(n)) $
$f = g$
$f(n) = O(g(n)) $
$f \leq g$
$f(n) = o(g(n)) $
$f \lt g$



Reference

MIT Lecture Notes: Big O notation

ratsgo’s blog, 점근 표기법(awymptotic notation)