List가 주어졌을 때 특정 값이 어느 index에 위치해 있는지 찾아내는 Task를 생각해보자.
선형탐색(Linear Search)
가장 간단하게 생각할 수 있는 방법은 선형 탐색(Linear Search)이다. 리스트의 첫 번째 요소부터 차례대로 해당 요소가 우리가 찾고 있는 요소와 같은지 확인한다. 만약 찾고 있는 요소와 같다면 탐색을 멈추고 index를 반환하고, 찾고 있는 요소와 다르다면 다음 요소를 확인하는 과정을 반복한다.
선형 탐색의 경우 리스트 길이에 비례하는 시간이 소요된다. 시간복잡도 $O(n)$
def linear_search(L, x): #L: list, x:the element we want to find.
l = 0 #lower bound
u = len(L)-1 #upper bound
idx = -1 #index of the element in list L. if x doesn't exists in L, returns -1
flag = x in L
while l != u+1:
if L[l] == x:
idx = l
break
else:
l += 1
return idx
이진탐색(Binary Search)
이진탐색은 오름차순으로 정렬 되어 있는 리스트에서 특정 값이 어느 index에 위치해 있는지 찾아낼 때 사용할 수 있다. 알고리즘의 특성 상 오름차순으로 정렬되어 있지 않으면 사용할 수 없다.
대학생때 술게임으로 많이 하곤 했던 업다운 게임을 생각해보자. 업다운 게임은 소주의 병뚜껑에 적혀 있는 숫자를 친구끼리 돌아가면서 맞춰보는 게임이다. 게임이 진행될수록 가능한 숫자의 범위가 줄어들게 되고, 결국 우리는 해당 숫자가 어느 숫자인지 알게 된다.
만약 혼자서 이 게임을 할 때, 가장 빠르게 끝낼 수 있는 방법은 무엇일까? 바로 가능한 숫자의 범위에서 항상 중위수(Median)만 부르는 방법이다. 이 방법은 자연수가 오름차순으로 정렬되어 있다는 사실(당연하다)을 활용하여 이진탐색을 사용한 것이라고 볼 수 있다.
자세한 예시는 아래 그림(출처: Wikipedia)을 통해 살펴보자.
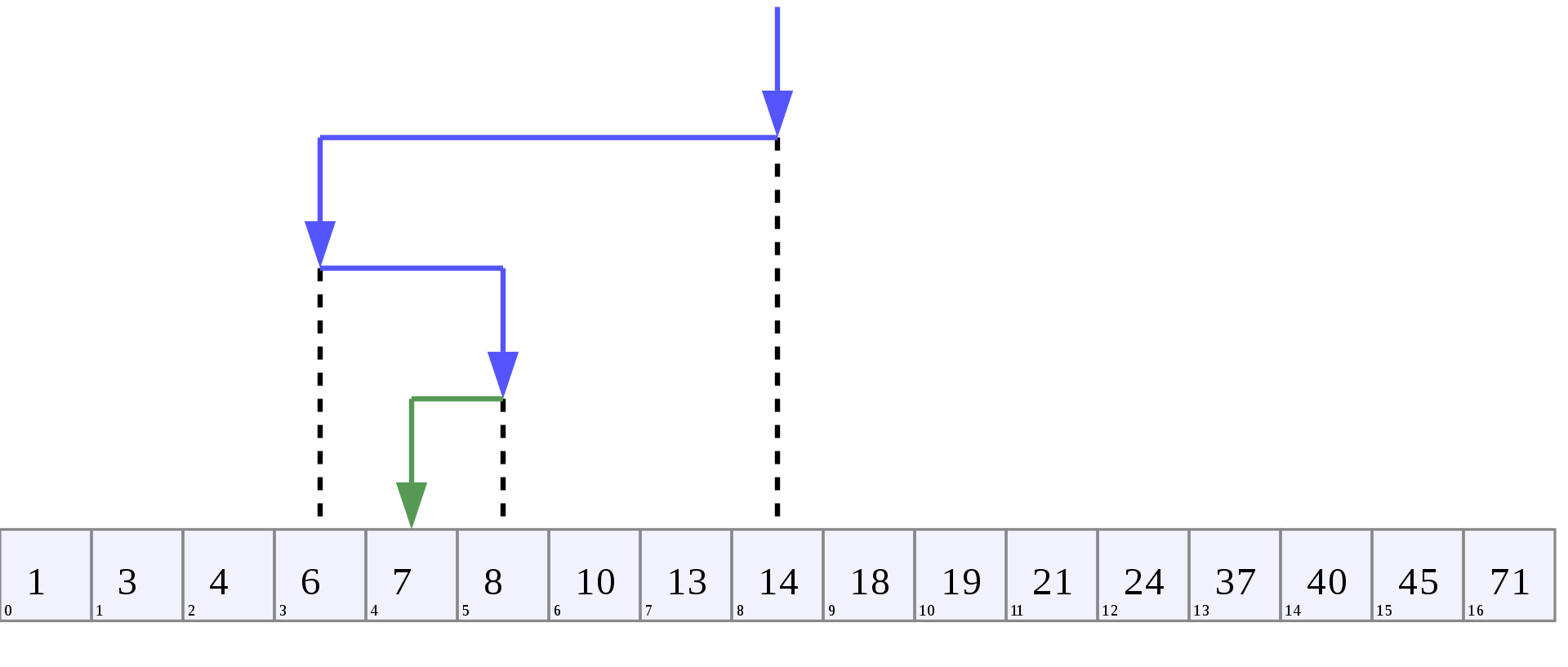
이 예시는 17개의 요소를 가진 list에서 특정 값 7의 index를 binary search를 통해 찾아내는 과정을 시각화한 것이다. 4번만에 찾아낸 것을 확인할 수 있다.
참고로 Binary Search 한 번 비교가 일어날 때마다 리스트가 반씩 줄어든다는 특징을 가지고 있다.(Divde&conquer property)
이진탐색의 경우 리스트의 log 길이에 비례하는 시간이 소요된다. 시간복잡도 $O(log(n))$
def binary_search(L, x): #L: list, x:the element we want to find.
l = 0 #lower bound
u = len(L)-1 #upper bound
idx = -1 #index of the element in list L. if x doesn't exists in L, returns -1
flag = x in L
while flag:
m = (l+u)//2
if L[m] == x:
idx = m
break
elif L[m]>x:
u = m
else:
l = m
return idx
비교
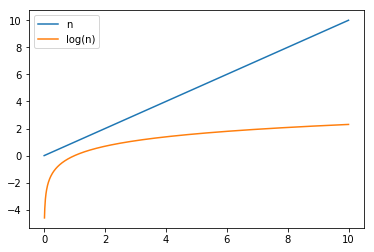
선형탐색의 $O(n)$과 이진탐색 $O(log(n))$의 차이가 얼마 나지 않는다고 생각할 수도 있다.
하지만 n이 매우 큰 경우에는 비교할 수 없는 차이가 생기게 된다.
4,294,967,296개(약 43억개)의 원소가 있는 리스트를 상상해보자.
리스트에서 특정 값을 찾아낼 때 이진탐색의 경우 Worst-case performance(최악의 탐색 깊이)는 딱 32번이다. 그러나 선형탐색의 경우 원하는 원소가 가장 마지막 요소인 Worst-case일 때 4,294,967,296번을 search해야 원하는 원소를 찾을 수 있다.
물론 Sorting되어 있어야 한다는 전제가 필요하지만 특정 케이스에서 $O(log(n))$의 Binary Search는 강력한 알고리즘이 될 수 있다.