트리(Trees)(1)

트리(Trees)

트리는 노드(node)와 엣지(edge)을 이용하여 데이터의 배치 형태를 추상화한 자료 구조이다. 스택/큐가 1차원의 자료구조였다면, 트리는 2차원의 자료구조이다.

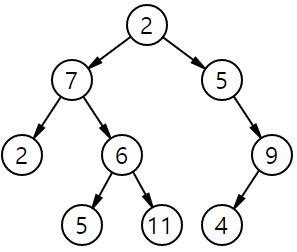
이 자료구조는 나무를 뒤집어 놓은 것과 비슷하여 트리라고 불리운다.

이번 포스트에서는 트리 자료구조를 공부하기 위하여 알아야 할 용어들에 대하여 살펴보도록 한다.

노드(Node)

뿌리쪽(즉, 위쪽)의 노드를 루트 노드(root node), 가장 마지막 노드는 리프 노드(leaf node), root도 leaf도 아닌 노드들은 인터널 노드(internal node)라고 한다.

각 node를 개별적으로 살펴보았을 때 뿌리 쪽(위 쪽)에 가까운 노드를 부모 노드(parent node), 잎 쪽(아래 쪽)에 가까운 노드를 자식 노드(child node)라고 한다. 같은 부모 노드에서 연결된 노드들은 서로 형제간 관계(sibling)에 있다고 말한다.

root 방향으로 올라가면서 만나는 모든 노드들은 조상(ancestor)이라고 하며, leaf 방향으로 내려가면서 만나는 모든 노드들은 후손(descendant)이라고 한다. 즉, root node의 입장에서는 자기 자신을 제외한 모든 노드들이 후손 노드가 된다.

수준(Level)

루트 노드로부터 해당 노드까지 도달하는데 거치는 간선의 수를 수준(level)이라고 한다. 예를들어, 위 그림에서 $11$에 해당하는 노드의 level은 3이 될 것이다.

따라서 루트 노드의 수준은 정의에 따라 0이 된다.(간혹 어떤 책에서는 1부터 시작하는 경우도 있지만, 일반적으로 0으로 하는 것이 맞다.)

높이(Height)

책에 따라 Height, 또는 Depth라고도 부른다.

트리의 높이(Height)는 다음과 같이 구할 수 있다.

따라서 위 예시 그림과 같은 트리에서의 Height는 4임을 알 수 있다.

부분 트리(Subtree)

트리에서 어느 한 노드를 기준으로 그 아래 방향으로 잘라내서 하나의 새로운 나무로 간주할 수 있다. 그러한 나무를 부분 트리(서브 트리)라고 한다.

노드의 차수(Degree)

어느 노드의 입장에서 봤을 때, 자신의 자식과 연결되는 간선의 수가 degree가 된다. 따라서 leaf 노드의 degree는 0이 된다.

이진 트리(Binary Tree)

모든 노드의 차수가 2이하인 트리를 Binary Tree라고 한다. 앞서 살펴보았던 예시 또한 이진 트리이다. 단, 비어있는 empty tree 또한 정의에 따라 이진 트리가 된다.

포화 이진 트리(Full Binary Tree)

모든 레벨에서 노드들이 모두 채워져 있는 이진 트리를 포화 이진 트리(Full Binary Tree)라고 한다. 이러한 정의 때문에 포화 이진 트리는 높이가 $k$라면 노드의 개수가 $2^k -1$이 된다.

완전 이진 트리(Complete Binary Tree)

높이가 $k$인 Full Binary Tree를 생각해보자.

이 때 $k-2$ level까지는 포화 이진트리이지만(모든 노드가 2개의 자식을 가짐),

만약 $k-1$ level에서는 왼쪽부터 노드가 순차적으로 채워져 있다면 이를 완전 이진 트리라고 한다.