이진 탐색 트리
모든 노드에 대하여 다음과 같은 성질을 만족하는 이진 트리 를 이진 탐색 트리 라고 한다.
-
왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작다.
-
오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 크다.
단, 중복되는 데이터 원소는 없는 것으로 가정한다.
활용
이진 탐색 트리를 가지고 있다면, 쉽게 데이터를 찾을 수 있다. 다음 이진 탐색 트리를 예시로 살펴보자.
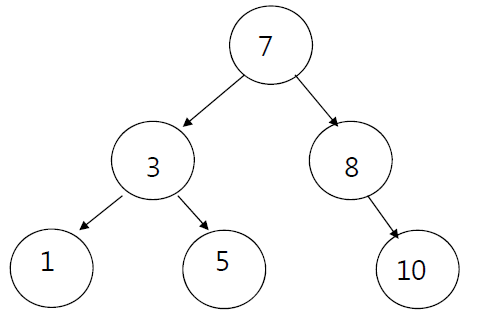
만약 여기서 5를 찾고자 한다면, 이진 탐색 트리는 아주 빠르게 찾아낼 수 있다.
루트 노드인 7에서 시작한다고 상상해보자. 5는 7보다 작으므로 왼쪽 subtree에 있거나, 혹은 트리에 데이터 자체가 존재하지 않을 것이다. 그 다음에는 3에 도달하는데 5는 3보다 크므로 오른쪽 subtree에 존재하거나, 해당 데이터 자체가 존재하지 않을 것이다. 따라서 오른쪽으로 이동하면… 5에 도달하게 된다.
배열을 이용한 이진 탐색과 비교
그런데 어디서 많이 본 듯한 내용이 아닌가?
사실, 배열을 이용한 이진 탐색(Binary Search)과 꽤 비슷하게 느껴진다. 하지만 비슷해 보여도 분명 차이가 있는 자료구조이다.
-
이진 탐색 트리(Binary Search Tree)는 정렬된 Binary Tree를 이용한다. 또한, Tree의 구조로 인하여 데이터 원소의 추가와 삭제가 용이하다는 장점이 있다.
-
이진 탐색(Binary Search)은 정렬된 배열을 이용한다. 반면, 데이터 원소의 추가와 삭제가 비효율적이다는 단점이 있다.
이렇게 보면 이진 탐색 트리(Binary Search Tree)가 이진 탐색(Binary Search)보다 월등히 좋아 보인다. 하지만, 이진 탐색 트리의 단점 또한 분명히 존재한다.
-
이진 탐색 트리의 경우 공간 소요가 크다는 단점이 존재한다.
-
이진 탐색 트리는 탐색시에 시간 복잡도 O(logn) 을 보장하지 못할 수도 있다.
이진 탐색 트리의 추상적 자료구조
이진 탐색 트리의 연산 정의는 다음과 같다.
- insert(key, data): 트리에 주어진 데이터 원소를 추가
- remove(key): 특정 원소를 트리로부터 삭제
- lookup(key): 특정 원소를 검색
- inorder(): 키의 순서대로 데이터 원소를 나열
- min(), max(): 최소 키, 최대 키를 가지는 원소를 각각 탐색
보다 나은 성능을 보이는 이진 탐색 트리
높이의 균형을 유지함으로써 O(logn) 의 턈색 복잡도를 보장하는 이진 탐색 트리도 있다.(이 경우, 삽입/삭제 연산이 보다 복잡하다.) 대표적인 예로 AVL tree, Red-black tree 등이 있다.