MCMC(2)-Gibbs sampling

Posterior가 간단한 형태를 가질 경우 Posterior로부터 쉽게 샘플을 구할 수 있을 것이고, Estimator 또한 쉽게 구할 수 있을 것이다. 하지만 만약 Posterior의 형태가 복잡하거나 Closed-form으로 구할 수 없는 경우 Sampling의 문제 또한 매우 어려워진다.

앞서 살펴본 MCMC의 대표적인 알고리즘인 Metropolis Hastings가 이러한 샘플링 문제를 해결하고자 고안된 알고리즘인데, 깁스 샘플러는 Metropolis Hastings 알고리즘의 Special case라고 볼 수 있다. 순차적으로 각 모수들의 조건부 확률 분포(Full conditional distribution)에서 모수들을 뽑아, 결국 사후분포로부터 샘플을 뽑아낼 수 있도록 해준다.

Gibbs Sampler

기본적인 깁스 샘플링의 과정은 다음과 같다.

모수 $\theta^{(t)} = (\theta_1^{(t)},\theta_2^{(t)},\cdots,\theta_k^{(t)})$를 생각해보자. 우리는 다음의 과정을 거쳐 $\theta$를 sampling할 수 있다.

Step 1: $\theta_1^{(t+1)} \sim p(\theta_1 \vert \theta_2^{(t)},\theta_3^{(t)},\theta_4^{(t)})$
Step 2: $\theta_2^{(t+1)} \sim p(\theta_2 \vert \theta_1^{(t+1)},\theta_3^{(t)},\theta_4^{(t)})$
Step 3: $\theta_3^{(t+1)} \sim p(\theta_3 \vert \theta_1^{(t+1)},\theta_2^{(t+1)},\theta_4^{(t)})$
Step 4: $\theta_4^{(t+1)} \sim p(\theta_4 \vert \theta_1^{(t+1)},\theta_2^{(t+1)},\theta_3^{(t+1)})$

위와 같은 step을 거쳐 $\theta$를 sampling할 수 있다.

Example

사실 처음 보았을 때에 직관적으로 이해하기가 쉽지만은 않을 것이다. 다음의 매우 간단한 예제를 살펴보면 훨씬 이해하기가 쉽다. 이 예시는 Joel Grus, Data Science from Scratch First Principles with python에서 가져온 예제다.

두 fair한 주사위 1,2를 생각해보자. 주사위 1의 눈을 $d_1$, 주사위 2의 눈을 $d_2$라고 하자.

우리는 두 확률 변수 $x$, $y$를 다음과 같이 정의하도록 하겠다.

$x$ = 두 주사위를 한 번 던졌을 때, 주사위 1에서 나오는 숫자. 즉, $d_1$과 같다.

$y$ = 두 주사위를 한 번 던졌을 때, 두 주사위에서 나오는 숫자들의 합. 즉, $d_1+d_2$와 같다.

물론 위 두 확률변수의 분포에서 $x$와 $y$를 샘플링하는 것은 아주 쉬운 일이지만, 간단한 경우를 통하여 깁스 샘플링을 이해해보고자 한다.

다음은 깁스 샘플링을 통하여 $(x,y)$를 샘플링하는 과정이다.

import numpy as np

def roll_a_die():
    num = np.random.choice(range(1,7))
    return num

def direct_sample():
    d1 = roll_a_die()
    d2 = roll_a_die()
    x= d1
    y= d1+d2
    return x, y

def random_y_given_x(x):
    y_sample = x + roll_a_die()
    return y_sample

def random_x_given_y(y):
    if y <= 7:
        x_sample = np.random.choice(range(1, y))
    else:
        x_sample = np.random.choice(range(y-6, 7))
    return x_sample

def gibbs_sampling(x,y,n_iters):
    for i in range(n_iters):
        x = random_x_given_y(y)
        y = random_y_given_x(x)
    return x, y

sampling 결과를 시각화해보면 다음과 같다.

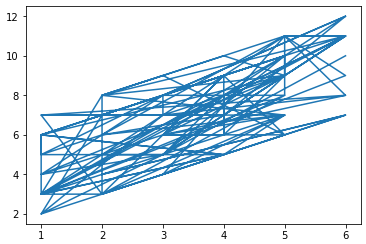
Gibbs sampling통하여 100번 sampling한 결과를 나타낸 것이다.

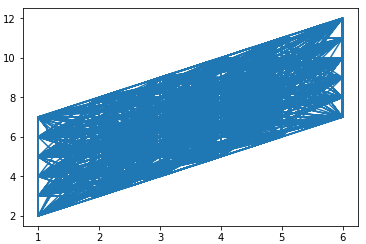
Gibbs sampling통하여 3000번 sampling한 결과를 나타낸 것이다.

이 때, 각각 x축과 y축의 방향에서 분포를 살펴보면 다음과 같은 모양이 나타난다.

우리는 직관적으로 $x$는 Uniform(1,6)의 분포를 따를 것이고, $y$는 7이 나올 확률이 가장 높으면서 1과 12 방향으로 갈 수록 줄어드는 분포를 가지고 있을 것이라 예상할 수 있다.

실제로 3000번 sampling한 경우에 대하여 $x$와 $y$ 각각의 히스토그램을 그려보면 다음과 같으며, 제대로 샘플링되었다는 것을 확인할 수 있다.

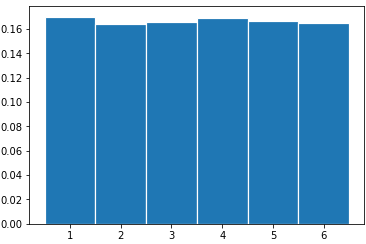
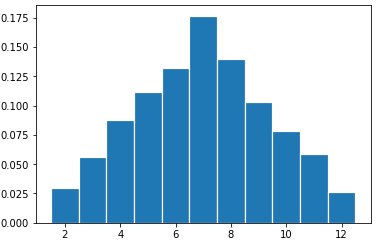
Reference

Sohn, Gibbs sampler란

ratsgo’s blog, Gibbs Sampling