BART(Bayesian Additive Regression Trees)

Related Post

BART(Bayesian Additive Regression Trees)

DART(Dirichlet Additive Regression Trees)

DART(2)-Backfitting MCMC

0. Introduction

Consider unkown function $f$ that predicts an output $Y$ using a $p$ dimensional vector of inputs $x=(x_1,\cdots,x_p) $

우리는 $f(x) = E(Y \vert X)$를 $h(x)$로 approximating 함으로써 $f(x)$를 모델링할 수 있다.

sum-of-trees 모델의 경우, 다음과 같이 모델링할 수 있을 것이다.

여기서 $g_j(x)$는 하나의 regression tree이다. A sum-of-trees 모델은 기본적으로 additive model with multivariate components 이다.

1. Notation

$T$는 하나의 Binary Tree model이다.

$b$는 $T$의 terminal nodes의 수이다.

$M = [\mu_1, \mu_2, \cdots, \mu_b]$는 T의 b개의 terminal nodes 각각의 parameter values이다.

$A$는 a subset of the range of $x$이다.

각 nodes에서의 spliting rule 은 {$x \in A$} vs {$x \notin A$}라고 하자. Continuous $x_i$의 경우, {$x_i \leq c$} vs {$x_i \gt c$}로 나타낼 수 있을 것이다.

2. A binary tree

각 $x$ value는 top부터 bottom까지 sequence of decision rules에 따라 하나의 terminal node와 관련되어 있고, 해당 노드의 parameter value $\mu_i$를 assign 받게 된다. 따라서 단일 tree 모델은 다음과 같이 나타낼 수 있다.(CGM98)

여기서 input $x$가 $g(x;T,M)$로부터 return 받는 output $\mu_i$는 $E[Y \vert x]$와 같다.

3. A sum-of-trees model

sum of trees 모델은 위와 같이 나타낼 수 있을 것이다.

이 모델에서 $E[Y \vert x]$는 모든 트리($j=1,2,…,m$)의 모든 terminal nodes($i=1,2,…,b$)의 parameter인 $\mu_{ij}$의 합과 같다.

각 트리는 주어진 $x$에 대하여 하나의 터미널 노드의 $\mu_i$를 예측 값으로 사용하고, 이러한 예측 값들을 $m$개의 각 트리마다 구하여 그 합을 구할 수 있다. 이는 $E[Y \vert x]$ 와 같다.

앞서 단일 tree와 조금 다른 점은 $\mu_{ij}$는 $E[Y \vert x]$의 일부분일 뿐 같지 않다는 것이다.

(참고)

$g(x;T_j, M_j)$가 하나의 변수에만 의존한다면 각 $\mu_{ij}$는 main effect를 나타낼 것이다.

반면, $g(x;T_j, M_j)$가 하나 이상의 변수에만 의존한다면 각 $\mu_{ij}$는 interaction effect를 나타낼 것이다.

즉, sum-of-trees model은 main effect와 interaction effect 모두를 포함하는 모델이다.

4. Prior: $T_j$, $M_j$ and $\sigma$

이제 $p(T_j)$, $p(\mu_{ij} \vert T_j)$, $p(\sigma)$의 세 priors의 specification이 필요하다.

이어서 살펴보겠지만, 우리는 이 세 가지 priors에 대하여 같은 priors forms를 사용한다.(proposed by CGM98 for Bayesian CART)

그 이유는 다음과 같다.

1. Computational benefits

2. These forms are controlled by just a few interpretable hyperparameters which can be calibrated using the data to yield effective default specifications for regularization of the sum-of-trees model

4.1. Prior: $T_j$

a. 첫 번째 Prior

depth(깊이) d의 한 노드가 non-terminal 일 확률은 다음과 같다.

b. 두 번째 prior

• 각 interior node에서 splitting variable 선택 에 대한 distribution

  Uniform prior on available variables

c. 세 번째 prior

• 각 interior node에서 splitting rule 선택 에 대한 distribution(conditional on splitting variable)

  Uniform prior on the discrete set of available splitting values

단일 tree 모델$(m=1)$의 경우, 많은 terminal nodes를 가질 경우 모델의 구조가 복잡하게 된다.

반면, sum-of-trees 모델$(m \geq 2)$의 경우, 각각의 tree components가 작도록 하기 위해서는 regularization prior가 필요하다.

논문에서는 simulation을 통해 alpha = 0.95, beta = 2를 사용하였다.

4.2. Prior: $\mu_{ij} \vert T_j$

For $p(\mu_{ij} \vert T_j),$ we use Conjugate Normal Distribution

이렇게 prior를 두는 이유는 $\mu_{ij}$를 marginalize out할 때 계산 상의 굉장한 이점이 있기 때문이다.

이제 hyperparameter인 $\mu_{\mu}$와 $\sigma_{\mu}^2$에 대해 조금 더 자세히 살펴보도록 하자.

$E[Y \vert x]$는 m개의 $\mu_{ij}$의 합이다.

$\mu_{ij} \overset{iid}{\sim} \cdot $ 이므로,

임을 알 수 있다.

우리는 $E[Y \vert x]$가 observed된 minimum과 maximum value of y 사이의 범위 $(y_{min}, y_{max})$에 있을 가능성이 높다는 것을 알고 있다.

우리의 전략은 $\mu_{\mu}$와 $\sigma_{\mu}^2$를 선택할 때 $N(m \mu_{\mu}, m \sigma_{\mu}^2)$이 interval $(y_{min}, y_{max})$에 substantial probability를 assign할 수 있도록 선택하는 것이다.

따라서 적당한 k를 정한 후, 다음을 만족하는 $\mu_{\mu}$와 $\sigma_{\mu}$를 구하도록 한다.

예를 들어, $k=2\;$: 95% prior probability that $E[Y \vert x]$ is in the interval $(y_{min}, y_{max})$

이 논문에서는 편리성을 위하여 먼저 $y_{min}=-0.5$, $y_{max}=0.5$에 $y$가 분포하도록 $Y$를 shifting & rescaling해주었다. 그렇게 한 후에 다음을 만족하는 $\mu_{\mu}, \sigma_{\mu}^2$를 정해준다.

따라서 최종적인 $\mu_{ij}$의 prior는 다음과 같다.

이 모델의 장점 중 하나는 transformation의 간결함이다. 독립변수의 linear combination을 사용하는 neural networks와 같은 모델의 경우 모든 $x$ 에 대한 standardization이 필요하다.

하지만 이 모델의 경우 tree splitting rule이 x에 대한 monotone transformation에 invariant하다는 성질 때문에 $y$ 에 대해서만 transformation해주면 된다.

4.3. Prior: $\sigma$

$\sigma$의 prior는 conjugate prior로 inverse chi-square distribution을 사용한다.

이 때 두 hyper parameter $\lambda$와 $\nu$에 대하여 살펴보도록 하자.

$\nu$($\chi^2$의 degress of freedom)의 경우, 분포의 적절한 모양을 위하여 3에서 10 사이에서 적절한 $\nu$를 선택하게 된다.

$\lambda$의 경우, ($q_{th}$ quantile of prior on $\sigma$)가 $\hat \sigma$에 located되도록 하는 $\lambda$를 선택한다. 여기서 이 $\hat \sigma$의 선택에는 크게 두 가지 방법이 있다.

첫 번째 방법은 비교적 naive한 방법으로, data $Y$의 sample standard deviatinon 을 선택하는 것이다.($ \hat \sigma = s$)

두 번째 방법은 linear model specification 이다. 이 방법은 $Y~X$의 linear regression에서 least squares로부터 residual standard deviation 을 $\hat \sigma$로 사용하는 것이다.

아래 그림은 quantile 값 $q$가 0.75, 0.90, 0.99에 따라 $\sigma$의 prior 분포를 그려본 것이다.

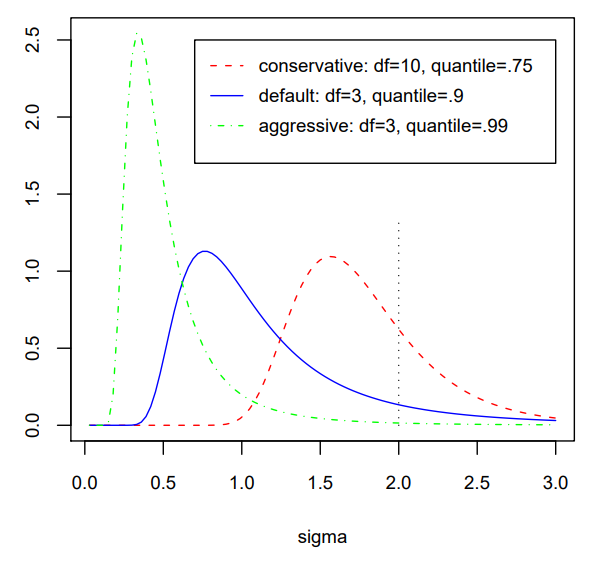
논문에서는 $\nu<3$의 $\nu$를 선택하는 것을 추천하지 않는다. 그 이유는 너무 작은 $\nu$ 값을 사용할 경우, 작은 $\sigma$에 대해 너무 큰 concentrate를 주게 되고, 이는 overfitting으로 이어질 수 있기 때문이다.

다양한 simulation을 통하여 default setting으로 ($\nu$, $q$)는 다음과 같이 정하며, 케이스마다 cross-validation을 통하여 적당한 값을 찾을 수 있다.

4.4. m: number of trees

Boosting 방법과 BART 방법은 여러개의 tree 모델을 통하여 estimate한다는 점에서 공통점을 가지고 있다.

하지만 major diffence는 number of trees: m에 대하여 BART는 m을 fixed value로 취급하지 않고, iterative backfitting algorithm 을 사용하여 m을 추정한다는 것이다.

BART는 m을 unknown parameter로 생각하며, m에 대해 추정하고자 한다.

크게 두 가지 방법이 있는데, 첫 번째로 m에 대한 prior를 주어 fully Bayes implementation할 수 있다. 두 번째 방법은 cross-validation을 통한 적절한 m 값을 선택하는 방법이다.

하지만 이 두 방법은 모두 계산상의 inefficiency가 매우 크며, 좋지 않은 방법이다.

Computational costs를 줄이기 위하여 이 논문에서는 tree의 개수 m의 선택에 대하여 다음과 같은 방법을 제시한다.

1. m=200을 default 값으로 사용한다.

2. default로부터 조금씩 m을 늘리거나 줄여가면서 결과의 변화에 영향을 주는지 확인한다.

3. 가장 좋은 성능을 보이는 적절한 m을 찾는다.

논문의 저자는 m=1부터 m을 증가시키면서 BART의 performance를 체크해보았는데, m이 커질수록 dramatical한 성능의 향상을 보였고, m이 적당히 커지고 난 이후에는 성능의 향상이 천천히 줄어들기 시작했다고 한다. 따라서 너무 작은 m은 선택하지 않는 것이 좋다. 굉장히 많은 dataset으로 실험해본 결과, m=200을 사용하는 것이 가장 좋은 예측 performance를 보여주었다.

Reference

Hugh A. Chipman, Edward I. George, Robert E. McCulloch(2008), BART: Bayesian Additive Regression Trees, Annals of Applied Statistics