DART(Dirichlet Additive Regression Trees)

0. Introduction

우선 DART에 대해 살펴보기 전에 Dirichlet Distribution에 대해 살펴보도록 하자.

1. Dirichlet Distribution

Dirichlet(디리클레) dist는 Beta dist의 multivariate 버전이다.

\[Dirichlet(x_1,\cdots,x_k\vert \alpha_1, \cdots, \alpha_k) = {1 \over B(\alpha)} \prod_{i=1}^k x_i^{\alpha_i -1}\] \[where\;B(\alpha)={\prod_{i=1}^k \Gamma(\alpha_i) \over \Gamma(\sum_{i=1}^k \alpha_i) }\]

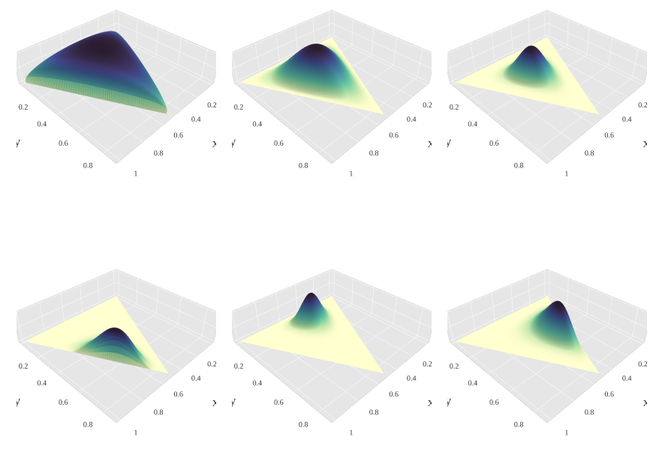
분포를 시각적으로 확인할 수 있도록 K=3인 경우의 분포를 확인해보면 다음과 같다. 왼쪽 위 그림부터 시계 방향으로 각각 (1.3,1.3,1.3), (3,3,3), (7,7,7), (2,6,11), (14,9,5), (6,2,6)를 모수로 가지는 Dirichlet 분포이다.

Dirichlet Distribution

2. DART

다음 nonparametric regression model을 생각해보자.

\[Y=f_0(X)+\epsilon_i,\;\;\;\epsilon_i \sim N(0, \sigma^2)\]

where $X$ taking values in $\mathbb{R}^p$

Sparsity assumption

$f_0(x)$ depends on $x$ only through $(x_q: q \in Q_0)$

where $Q_0 \subseteq$ {$1,\cdots,P$}

and the size of $Q_0$ is assumed to be much smaller than P.

즉, $X_1,\cdots,X_p$의 P개의 변수들 중 일부분의 변수($Q_0$)들에만 $f_0(x)$가 의존하도록 하는 $Q_0$가 있다고 하자. 여기서 $Q_0$는 원소의 개수가 P개보다 훨씬 적은 수의 집합이다.

모델 $f_0(x)$에 대한 가정이 합리적이라면, 우리는 적절한 $Q_0$를 찾아내야 한다.

다음을 통해 do not generally adapt to sparsity 한 예시를 생각해보자.

예시)

\[f_0(x) = 10 sin(\pi x_1 x_2)+20(x_3 - 0.5)^2 + 10x_4 + 5x_5\] \[where\;observation(N\;by\;P)\; has\;\; \begin{cases} N=100\\ (P-5) \text{ irrelevant predictors}\\ \sigma^2 = 1 \end{cases}\]

변수 X의 개수 P가 각각 10, 100, 1000개일 때를 생각해보자. ($P \in$ {$10, 100, 1000$})

이 때 BART, DART, RandomForests의 성능을 비교해보면 다음과 같다. 가로 축은 $\mu$이며, 세로 축은 $\hat \mu$이다.

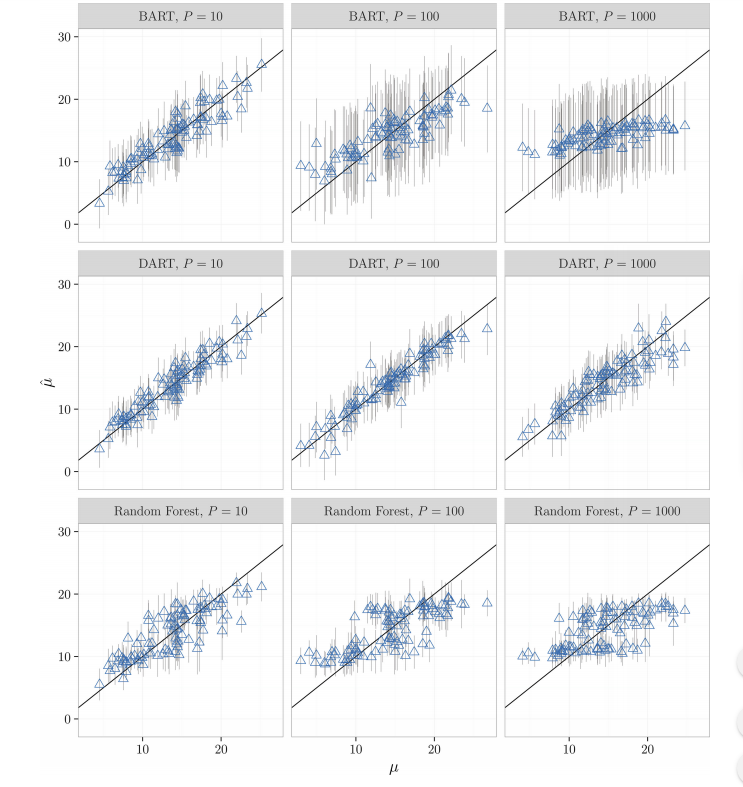
[Plot of the true mean $f_o(x) = \mu$ against the estimated mean $\hat f(x) = \hat \mu$]

RandomForests와 BART의 경우 P가 커지면서 성능이 급격하게 떨어지는 것을 확인할 수 있다.

특히, 극단적으로 P=1000인 경우, BART는 모든 예측 값 $\hat Y$을 표본 평균 $N^{-1}\sum_i Y_i$로으로 rough하게 예측하게 된다. RandomForests 또한 비슷한 양상을 보인다.

반면 DART의 경우 많은 nuisance 변수들의 존재에 대해 상당히 robust한 모습을 보여준다.(DART is resilient to the presence of large numbers of nuisance predictors.)

$s$: sparsity inducing Dirichlet prior

Bayesian Approach는 해당 모델을 랜덤하게 선택된 변수의 값(values)에 따라 재귀적으로 노드를 나누는 과정 으로 만들어진 random trees의 앙상블 모델이라는 관점에서 접근하게 된다.

변수 $X_j$가 주어진 노드 분할에 사용되는 확률을 $s_j$라고 하고, $s=(s_1, \cdots, s_p)$라고 하자.

BART와 같은 일반적인 모델에서는 $s_j = {1 \over P}$를 가정하여 모든 P개의 변수들이 Uniformly 선택되도록 한다.

반면, DART에서는 $s$에 대한 분포를 sparsity-inducing Dirichlet distribution로 가정한다.

\[(s_1,\cdots,s_p) \sim Dirichlet({\alpha \over P}, \cdots, {\alpha \over P})\]

Adaptivity to sparsity

$s$의 분포에 대하여 $Dirichlet$ 분포를 가정한다면, 우리는 함수 $f_0(x)$에서 adaptivity to sparsity 를 얻을 수 있다.

다음 그림을 살펴보자.

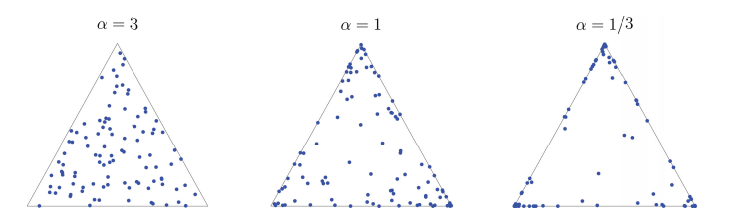
[Draws from $Dirichlet({\alpha \over 3},{\alpha \over 3},{\alpha \over 3})$, $\;where\;\alpha = 3, 1, 1/3$]

이 그림에서 $\alpha \over P$가 작을 때 data의 분포가 sparse하게 되는 것을 확인할 수 있다.

즉, BART에서 splitting rule에 대한 prior에 Dirichlet distribution을 주면 이러한 변수들의 Sparsity에 대해 잘 컨트롤할 수 있게 되는 것이다.(쉽게 말하면, 필요 없는 변수들이 Sparse하게, 즉 선택되지 않도록 유도하는 것이다.)

이렇게 Dirichlet dist를 BART framework에 포함시키게 되면, Dirichlet splitting rule prior는 다양한 advantages를 가지게 된다.

우선, 변수 선택의 측면에 있어서 장점을 가진다. 기존의 BART based 모델의 경우, Fully Bayesian Approach를 버리고 Variable Importance에 대하여 촛점을 맞춘다. 반면, DART의 경우 fully Bayesian Approach를 통하여 변수 선택을 하게 된다.

이에 더하여, 기존의 BART based 모델의 경우 적은 수의 나무를 사용하도록 제한하여 성능의 저하를 가져온다. 하지만 DART는 tree의 개수에 제한을 두지 않는다는 장점이 있다.

Reference

Antonio R. Linero(2016), Bayesian Regression Trees for High-Dimensional Prediction and Variable Selection, Journal of the American Statistical Association

Related Post