Estimating cdf $F$
우리가 어떠한 데이터를 가지고 있다고 가정하자. 대부분 우리는 그 데이터의 모집단에 대한 정보가 없지만, 우리가 가지고있는 데이터만으로 모집단의 분포를 Estimate할 수 있다면 아주 유용할 것이다. 우리가 추정하고자 하는 확률변수의 pdf를 f, cdf를 F라고 하자. 이번 포스트에서는 EDF를 통해 cdf $F$를 간단하게 추정하는 방법에 대해 살펴보겠다.
Empirical Distribution Function
우리는 n개의 데이터를 가지고 있고, 이 데이터를 $\left \lbrace {X_j}\right \rbrace ^n_{j=1}$라고 나타내자. 이 데이터의 cdf $F$를 Estimate할 수 있는 Empirical한 cdf를 다음과 같이 생각해볼 수 있다.
\[F_n(x) = {1 \over n} \sum^n_{j=1} I(X_j \leq x)\]이 Empirical cdf $F_n$은 $F$에 대한 좋은 estimator가 될 수 있다. 하지만 주의해야 하는 점은 $dF_n \over dx$은 $f={dF \over dx}$의 좋은 estimator가 아니라는 점이다. 그 이유는 $dF_n/dx$는 모든 $x_i$ 에서 $1/n$이라고 정의할 수 밖에 없는데 이 경우 entropy 추정량인 $-\sum p_i log(p_i)$ 를 구한다면 어떠한 모집단의 표본에 대해서 $log (n)$으로 똑같이 추정되어버려 분포의 특성을 반영하지 못하게 되기 때문이다.
EDF Source code
def EDF(data, x):
n = len(data)
estimated_cdf = 1/n*sum(data <= x)
return(estimated_cdf)
Example: Yellowstone National Park dataset
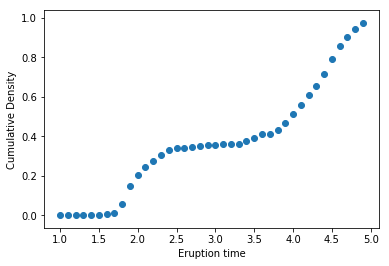
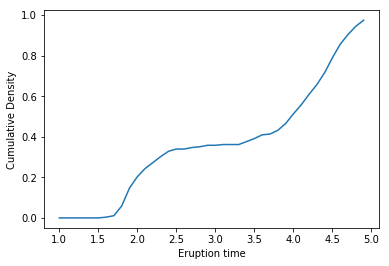
이 예시는 Eruption times and waiting times (in minutes) of consecutive eruptions of the Old faithful geyser in Yellowstone National Park에 대한 데이터셋이다. Eruption time에 대한 분포를 추정하고자 하는데, 이번 예제에서는 Empirical Distribution Function을 통하여 cdf를 추정해 보면 다음과 같다.
Reference
Sangun Park(2019), Nonparametric Statistics: Nonparametric Density Estimation, Yonsei University