우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 모두를 위한 딥러닝 시즌2의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
Optimization
Regression model이나 이를 기반으로하는 어떠한 신경망 모형이든 결국 Cost를 정의하고, 이를 Minimize하는 parameters를 추정하는 것이 Regression/Classification 모형의 목적이 된다. 이러한 Cost(혹은, MSE)의 최소화는 미분(Differentiating)을 기반으로 이루어지는데, 이러한 과정을 조금 더 자세히 살펴보도록 하겠다.
예시를 통하여 살펴보면 이해가 빠르므로, 앞서 살펴본 Linear regression의 예제를 기반으로 설명하도록 하겠다.
### Linear Regression
# Dataset
X_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# Weight Initialization
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# Setting Optimizer
optimizer = torch.optim.SGD([W, b], lr=0.01)
# Training
n_epochs = 2000
for epoch in range(n_epochs + 1):
# H(x)
hypothesis = X_train * W + b
# cost
cost = torch.mean((hypothesis - y_train) ** 2)
# Updating W, b
optimizer.zero_grad() # Initialize Gradients calculated in the last step.
cost.backward() # Getting new Gradients based on Differentiating of this step.
optimizer.step() # Update W, b with new Gradients(& learning_rate)
# print
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, n_epochs, W.item(), b.item(), cost.item()
))
여기서는 torch.optim.SGD를 사용하여 optimizer를 정의한 뒤, Gradient를 0으로 초기화하고(optimizer.zero_grad()), 모수들에 대한 Cost의 새로운 Gradient를 계산하여(cost.backward()), 모수들을 Update 해주는 과정을(optimizer.step()) 매 Epoch마다 반복하고 있다.
Cost
우리는 Hypothesis 모형을 $Wx+b$로 가정하는 Simple Linear Regression 문제를 풀고있으며, 이에 따른 Cost function은 다음과 같다.
\[\begin{align*} H(x) &= Wx + b\\ cost(W, b) &= \frac 1 n \sum^n_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2\\ &= \frac 1 n \sum^n_{i=1} \left( (Wx^{(i)} + b) - y^{(i)} \right)^2 \\ \end{align*}\]우리가 관심을 가지는 모수는 W와 b이며, Cost를 minimize하는 최적의 W와 b를 찾는 것이 Regression 및 다양한 신경망의 최종 목표이다. 이러한 최적의 W와 b를 찾는 과정을 Optimization이라고 할 수 있는데, 기초적인 Gradient Descent를 비롯한 다양한 Optimization 방법이 논의가 되었고, 많이 사용되고 있다. 그 중, 이번 포스트에서는 Gradient Descent 방법에 대해 살펴보고자 한다.
이제 풀고자 하는 문제로 다시 돌아가보자.
import torch
import numpy as np
import matplotlib.pyplot as plt
# Dataset
X_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
plt.scatter(X_train, y_train)
plt.show()
xs = np.linspace(1, 3, 1000)
plt.plot(xs, xs)
plt.show()
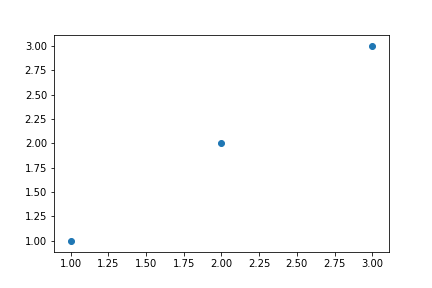
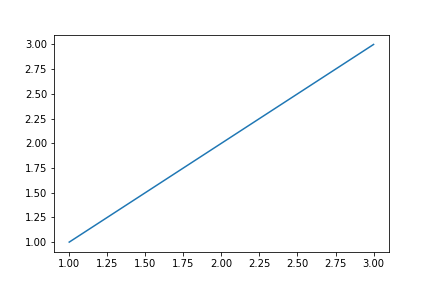
Training data는 왼쪽의 scatter plot과 같이 분포하고 있으며 우리는 regression 문제를 풂으로써 training data를 가장 잘 설명하는, 오른쪽의 이상적인 line을 찾고자 한다.
사실 우리는 최적의 모형을 찾기 위하여 W와 b 모두에 관심을 가지고 있지만, 최대한 간단한 설명을 위하여 우선 b를 0으로 고정한 뒤에 W에 대한 최적의 값을 찾는 문제로 살짝 변형해 보자. 이제부터 우리의 목표는 Cost를 Minimize하는 최적의 W를 찾는 것이다.
# W vs Cost
W_l = np.linspace(-5, 7, 1000)
cost_l = []
b = 0 # Assumet that b is fixed
for W in W_l:
hypothesis = W * X_train + b
cost = torch.mean((hypothesis - y_train) ** 2)
cost_l.append(cost.item())
plt.plot(W_l, cost_l)
plt.xlabel('$W$')
plt.ylabel('Cost')
plt.show()
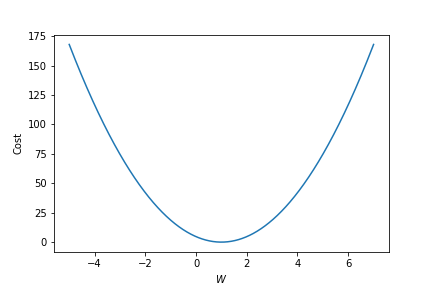
우리가 가정한 모형에서 W의 변화에 따른 Cost의 변화를 나타낸 Plot이다. $W$가 1일 때 가장 Cost가 줄어드는 것을 시각적으로 확인할 수 있다.(우리가 풀고 있는 문제는 아주 간단한 예시로써, cost를 정의하고 optimization을 통하여 $W$를 찾지 않더라도 직관적으로 $W = 1$일 때 가장 이상적인 모형이 된다는 것을 알고 있다.)
하지만 문제가 복잡해지면 Plot을 통하여 직관적/시각적으로 최적의 $W$를 찾는 것은 불가능하며, 우리는 다양한 optimization 방법을 통하여 최적의 $W$를 찾게 된다. 이번 포스트에서는 가장 기본적인 optimization 방법인 Gradient Descent 방법을 사용하여 최적의 $W$를 찾아볼 것이다. 그러기 위해서 우선 Gradient Descent가 무엇인지에 대하여 먼저 살펴보도록 하겠다.
Gradient Descent
우리는 주어진 Cost function에서 Cost를 최소화 시키는 $W$를 찾는 것이 목표이다. 즉, 어떠한 함수($f(x)$)에서 그 함수를 최소화하는 $x$를 찾는 것이 목표인 것이다. 간단한 설명을 위하여 $y=(x-1)^2$을 최소화하는 $x$를 찾는 문제를 생각해보자.
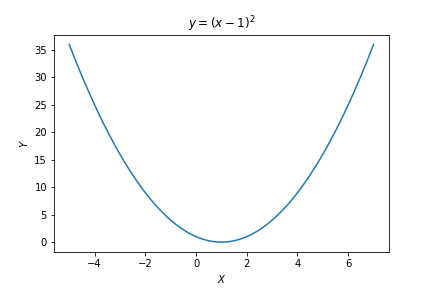
Gradient(기울기)란 벡터 미적분학에서 스칼라장의 최대의 증가율을 나타내는 벡터장을 뜻한다. Gradient Descent Optimization은 $y$의 $x$에 대한 Gradient, 즉 미분값 $f(x)’$를 활용하여 최적의 $x$를 찾는다. 우선 $y=f(x)$의 미분 함수를 구해보자.
\[\begin{align*} y &= (x-1)^2\\ y' &= \frac {\partial y}{\partial x} = 2 (x-1) \cdot 1\\ \end{align*}\]Gradient Descent optimization을 사용하기 위해서는 $x$에 대한 초기값을 부여해야 한다. 초기값을 $x=3$으로 부여했다고 하자.
(사실 우리가 풀고 있는 문제와 같이 간단한 regression 문제에서는 x를 어떠한 값으로 initialize하여도 크게 상관이 없지만, 상당히 복잡한 문제를 풀어야 하는 대부분의 Deep learning 모형에서는 $x$에 대한 초기값을 어떻게 주는가가 optimization에 상당히 큰 영향을 미친다. 실제로 Initialization 문제 또한 다양한 해결방법이 논의되고 고안되었다.)
$x=3$에서의 미분값을 구해보면 다음과 같다.
\[\begin{align*} \frac{\partial y}{\partial x}\vert _ {x=3} &= 2 (3-1) \cdot 1\\ &= 4 \end{align*}\]아래 plot에서 확인할 수 있듯이 $x=3$에서의 미분 값, 즉 기울기(Gradient)는 4이며, $x=3$에서 $f(x)$의 접선의 기울기 또한 4이다.
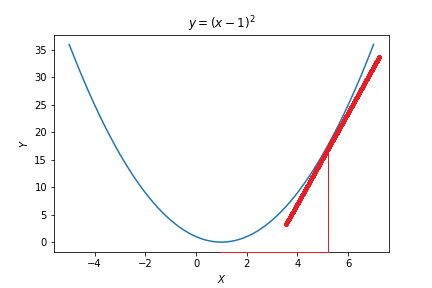
Gradient 값이 4로써 양수인데, 이를 통하여 우리는 $x=3$에서 $x$가 한 단위 증가 할 때 $f(x)$가 4만큼 증가 한다는 사실을 알 수 있다. 바꿔 말하면, $x=3$에서 $x$가 한 단위 감소 할 때 $f(x)$가 4만큼 감소 한다는 것이다.
우리의 목표는 $f(x)$를 감소 시켜서 최종적으로 최소값에 도달하는 것이다. 즉, $f(x)$를 최소화하는 $x$를 찾아야 하므로, $x=3$에서의 Gradient가 4인 것으로부터 $x$를 3보다 조금 더 감소시켜야 한다는 사실을 알 수 있다.
조금만 더 생각해보면, 특정 $x$에서의 Gradient가 양수라면 $x$를 감소시키고, Gradient가 음수라면 $x$를 증가시키는 과정을 지속적으로 반복했을 때 결과적으로 $f(x)$를 최소화시킬 수 있다는 사실을 깨달을 수 있다. 여기서 핵심은 $f(x)$를 최소화 시키고자 할 때 Gradient의 부호의 반대 방향 으로 $x$를 update해줘야 한다는 것이다.
이제 $x$를 얼마나 많이 감소, 혹은 증가시킬 것인가에 대한 문제가 남아 있는데, 이 문제는 Gradient의 절대값으로부터 해결할 수 있다. 특정 $x$에서의 Gradient(기울기)의 절대값이 크면 그 만큼 최적의 $x$와 멀다는 뜻이고, 기울기의 절대값이 작으면 그 만큼 최적의 $x$와 가깝다는 뜻으로 해석할 수 있다. 즉, 아래 그림과 같이 Gradient의 절대값이 크면 $x$를 많이 변화시켜주고, 절대값이 작으면 $x$를 적게 변화시켜주면 되는 것이다.

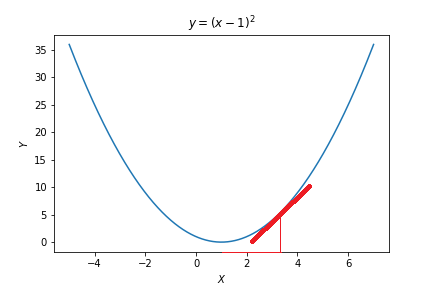
최종적으로 이러한 사실들을 반영하여 Gradient Descent는 다음과 같은 규칙으로 $x$를 update한다.
\[x_{new} = x_{old} - \alpha \cdot \frac{\partial y}{\partial x}\vert _ {x=x_{old}}\]여기서 상수 $\alpha$는 learning rate이라고 부르며, 최적의 $x$로 잘 수렴할 수 있도록 적절한 값을 선택하여 사용하면 된다.
Example
다시 앞으로 돌아가보자. 우리가 풀고 있었던 Regression 문제의 cost function은 다음과 같이 정의된다.(b=0 가정)
\[\begin{align*} H(x) &= Wx + b\\ cost(W, b) &= \frac{1}{n} \sum^n_{i=1} \left( H(x^{(i)}) - y^{(i)} \right)^2\\ &= \frac{1}{n} \sum^n_{i=1} \left( Wx^{(i)} - y^{(i)} \right)^2 \\ \end{align*}\]사실 Cost를 minimize하는 $W$와 $b$를 찾는 것이 목표일 때, 이를 해결하는 하나의 방법은 Cost function을 $W$와 $b$에 대하여 미분한 결과가 0이 되도록 하는 $W$와 $b$를 찾는 것이다. 이러한 방법이 통계학에서 사용되는 OLS(Ordinary Least Squares) method이다.
Gradient Descent는 이와 다르게 여러 Step을 거쳐 지속적으로 $W$와 $b$를 조금씩 update함으로써 true $W$와 $b$에 근사(Approximate)시키는 방법이다. 다음과 같이 Cost를 $W$에 대하여 미분해 보자.
\[\begin{align*} \nabla W &= \frac{\partial cost}{\partial W}\\ &= \frac{2}{n} \sum^n_{i=1} \left( Wx^{(i)} - y^{(i)} \right)x^{(i)} \end{align*}\]Gradient Descent Optimization은 매 Epoch마다 다음과 같이 $W$의 추정치를 지속적으로 Update 함으로써 True $W$에 가까워지도록 만든다.
\[W_{new} = W_{old} - \alpha \nabla W\]이제 실제로 계산해보도록 하자. Cost 함수는 다음과 같이 정의된다.
# cost
cost = torch.mean((hypothesis - y_train) ** 2)
$W$에 대한 초기값을 2으로 주었을 때 Gradient를 계산해보면 9.333인 것을 알 수 있다.
W = 2
gradient = 2/n*torch.sum((W * X_train - y_train) * X_train)
print(gradient)
$W=2$에서 구한 gradient를 사용, W를 아래와 같이 update해주어 새로운 $W = 1.533 $을 구한다.
lr = 0.05
W -= lr * gradient
print(W)
해당 과정을 충분한 수 만큼 반복하여 최적의 $W$를 찾아가는 과정이 Gradient Descent optimization이다.
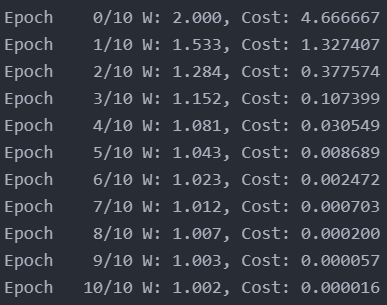
Source code
import torch
import numpy as np
import matplotlib.pyplot as plt
### Linear Regression
# dataset
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
n = x_train.size()[0]
# Weight Initialization
W = torch.FloatTensor([2])
# learning rate
lr = 0.05
# Training
n_epochs = 10
for epoch in range(n_epochs + 1):
# H(x)
hypothesis = x_train * W
# cost/gradient
cost = torch.mean((hypothesis - y_train) ** 2)
gradient = 2/n*torch.sum((W * x_train - y_train) * x_train)
#print
print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
epoch, n_epochs, W.item(), cost.item()
))
# Updating W with gradient
W -= lr * gradient
Reference
CS231n, Stanford University School of Engineering