우선, 해당 포스트는 Stanford University School of Engineering의 CS231n의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
GD(Gradient Descent)
앞선 Optimization(1)-Gradient Descent 포스트에서 Gradient Descent 포스트에 대하여 살펴보았다. Gradient Descent optimization는 weight을 한 번 update하기 위하여 다음과 같은 계산 과정이 필요하다.
\[L(W) = \frac 1 N \sum_{i=1}^N L_i(x_i, y_i, w)\] \[\nabla_W \cdot L(W) = \frac 1 N \sum_{i=1}^N \nabla_W L_i(x_i, y_i, w)\]Gradient Descent를 사용할 경우 한 가지 문제점이 발생하게 되는데, 매 iteration의 계산마다 $N$개의 training data를 모두 사용하여 계산해야 한다는 점이다. 즉, computational cost가 상당히 expensive하다는 것이다.
앞의 예시처럼 data의 수가 상당히 적을 때에는 문제가 되지 않지만, data의 크기가 아주 커지면 수렴 속도가 상당히 느려지게 된다.
SGD(Stochastic Gradient Descent)
GD(Gradient Descent)의 문제점을 보완한 optimization 방법이 바로 SGD(Stochastic Gradient Descent) optimization이다.
SGD는 true gradient를 estimate하기 위하여 $N$개의 데이터 모두를 사용하여 loss의 gradient를 계산하는 것이 아닌, 각 iteration마다 traning data의 small set을 sampling(mini batch)한 후, 해당 mini batch에 대한 loss와 gradient를 계산하게 된다.
이러한 방법에 ‘Stochastic’이라는 이름이 붙은 이유는 SGD를 Monte Carlo estimate로 볼 수 있기 때문이다.
SGD의 pseudo-code는 다음과 같다.
while True:
weights_grad = evaluate_gradient(loss_function, data, weights)
weights += -step_size * weights_grad
하지만 SGD 또한 여전히 여러 문제가 존재하는데 크게 3가지 문제점을 살펴보도록 하겠다.
problem 1. Differnt sensitivities of the weights
첫 번째 문제는 각 weight의 변화가 loss 감소에 미치는 영향이 weight마다 다르고, 이 때문에 zigzaging behavior가 나타나 속도가 여전히 느리다는 것이다. 다음 예시 그림을 보면 훨씬 이해하기가 쉽다.
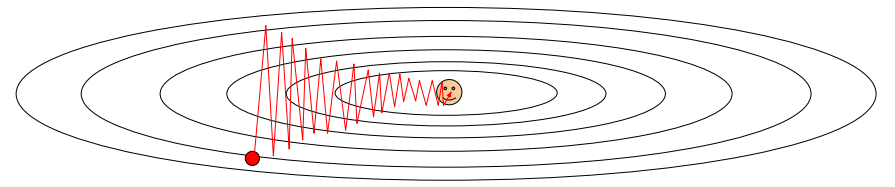
이 예시에서는 가로 방향으로는 해당 축에 해당하는 weight이 변함에 따라 loss가 상당히 느리게 바뀌며, 해당 weight는 not sensitive하다는 사실을 알 수 있다. 반면, 세로 방향으로는 loss가 아주 빠르게 변화하며, 해당 weiht이 상대적으로 더 sensitive하다는 것을 알 수 있다.
이러한 상황에 대하여 우리는 이 point에서 loss가 bad condition number를 가지고 있다고 표현한다. Condition number란 Hessian Matrix의 singular value의 가장 큰 값과 가장 작은 값 간의 비율을 의미한다. 이러한 경우, SGD의 performance는 상당히 좋지 않다.
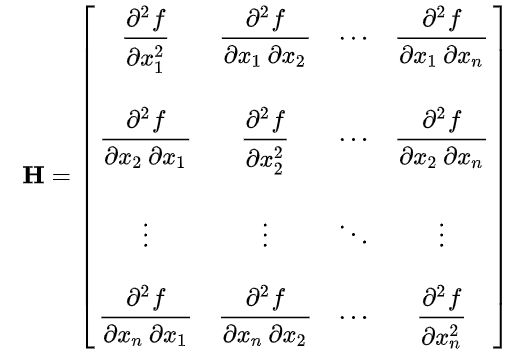
위 예시는 2차원의 optimization landscape를 보여주고 있지만 고차원의 경우 이러한 문제는 훨씬 더 빈번하게 발생한다.
problem 2. local minimum/saddle point
SGD는 매 iteration마다 gradient와 step in the direction of opposite gradient를 계산하게 된다. 그런데 만약 global optimal point가 아닌 지점에서 gradient가 0으로 계산되는 경우, 해당 지점에서 weight update가 멈추게 되고 우리는 원하는 결과를 얻을 수 없게 된다. 다음 그림을 살펴보자.
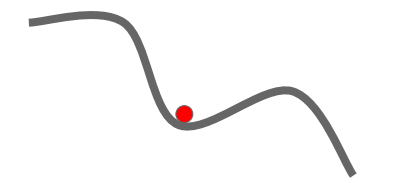
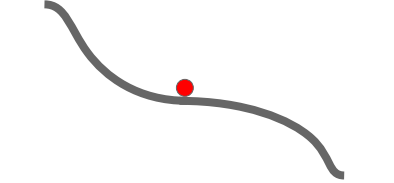
우리는 왼쪽의 경우를 local minimum, 오른쪽의 경우를 saddle point라고 말한다.
local minimum에서는 어떠한 방향으로 weight이 움직이더라도 loss가 증가하게 되어, 그 시점에서 update가 중단되게 된다. 사실 local minimum의 경우 high dimension에서는 자주 발생하는 문제는 아니다.
saddle point의 경우 역시 gradient가 0으로써 update가 이루어지지 않게 된다. 무엇보다 saddle point의 가장 큰 문제점은 saddle point 주변의 기울기는 0은 아니지만 거의 0에 가까운, 아주 작은 Gradient를 가지고 있기 때문에 update가 상당히 느리게 진행된다는 것이다. saddle point의 문제는 high dimension에서 상당히 자주 일어나게 되는 일이며 거의 모든 고차원 문제에서 겪게되는 문제점이다.
problem 3. noise
“Stochastic”하다는 특성 때문에 noise가 존재하는 경우, 아래 그림에서 볼 수 있듯이 performance가 좋지 않을 수 있다.
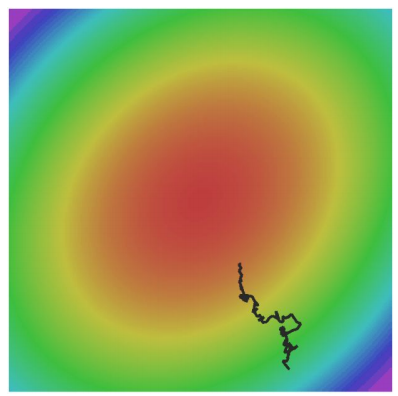
SGD with Momentum
SGD는 다음과 같이 weight을 업데이트 한다.
\[w_{t+1} = w_t - \alpha \cdot \nabla f(w_t)\]#pseudo-code for SGD
while True:
dw = compute_gradient(w)
w += -learning_rate * dw
앞서 살펴본 SGD의 여러 문제들을 해결하는 방법으로 다음과 같이 Momentum의 개념을 도입하게 된다.
\[\begin{align*} v_{t+1} &= \rho v_t + \nabla f(w_t)\\ w_{t+1} &= w_t - \alpha \cdot v_{t+1}\\ &= w_t - \alpha (\rho v_t + \nabla f(w_t))\\ &= w_t - \alpha \cdot \nabla f(w_t)- \alpha \cdot \rho v_t \end{align*}\]#pseudo-code for SGD with momentum
vw = 0
while True:
dw = compute_gradient(w)
vw = rho * vw + dw
w += -learning_rate * vw
v는 velocity, $\rho$는 friction이라고 하며, $\rho$의 경우 일반적으로 0.9, 0.99와 같은 값을 사용한다.
즉, 해당 point에서 마찰계수(friction)를 반영한 속도(velocity)를 먼저 계산하고, 이를 weight update에 사용하는 것이다.
이러한 설정으로 경사 낮은 지점에서는 변하는 속도가 느리게, 경사가 가파른 지점에서는 변하는 속도가 빠르게 만들어 줄 수 있다.
이렇게 momentum을 도입하게 되면 SGD의 문제점들을 해결할 수 있게 된다. 우선, not sensitive한 방향으로 계속 velocity가 더 붙게되고, 이로 인하여 더 많이 이동하게 된다. 또한 gradient가 순간적으로 0이 되더라도 momentum 덕분에 극복이 가능하게 되며, noise 또한 averaged out되어 optimal minimum으로 훨씬 더 smooth하게 수렴이 이루어진다.
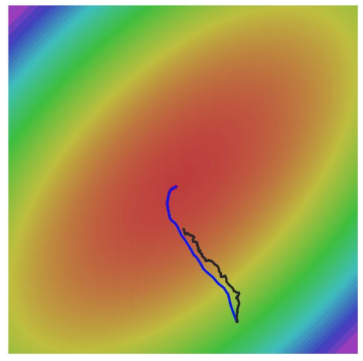
단, Velocity를 활용하는 momentum의 특성 상 처음에는 overshooting이 발생할 수 있지만, 결과적으로는 SGD보다 훨씬 더 빠르게 optimal point에 도달하게 된다.
NAG(Nesterov Accelerated Gradient)
SGD with momentum을 조금 더 개선한 optimization 방법이다. SGD with momentum과 거의 비슷한데 Gradient를 계산하는 순서만 조금 바꾼 형태를 가지며, convergence가 더 좋음이 이론적으로 증명되어 있다.
\[\begin{align*} v_{t+1} &= \rho v_t + \nabla f(w_t + \rho v_t)\\ w_{t+1} &= w_t + v_{t+1}\\ \end{align*}\]우리는 편리함을 위하여 이 식을 $x_t$와 $\nabla f(x_t)$로 나타낼 수 있도록 변형할 것이다. $\tilde w_t = w_t + \rho v_t$로 두고 식을 조금 더 정리해보면 다음과 같다.
\[\begin{align*} v_{t+1} &= \rho v_t + \nabla f(\tilde w_t)\\ \tilde w_{t+1} &= \tilde w_t - \rho v_t + \rho v_{t+1} + v_{t+1}\\ &= \tilde w_t + v_{t+1} + \rho ( v_{t+1} - v_t)\\ &= \tilde w_t -\rho v_t + (1+\rho)v_{t+1}\\ \end{align*}\]#pseudo-code for NAG
vw = 0
while True:
dw = compute_gradient(w)
old_v = v
v = rho * v - learning_rate * dw
w += -rho * old_v + (1+rho) * v
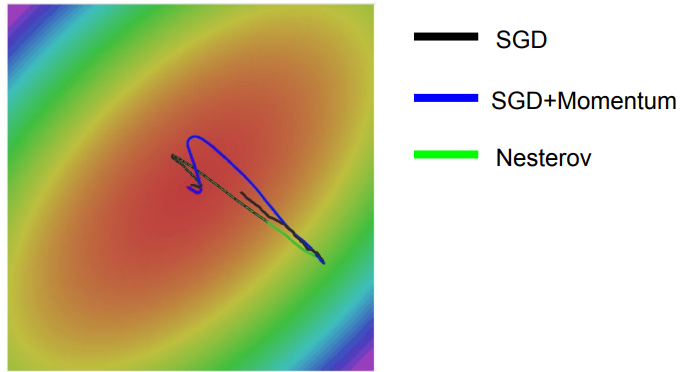
그림에서 확인할 수 있듯이, Nesterov가 SGD, SGD+Momentum보다 훨씬 빠르게 수렴하고 있다. 다만, Nesterov 역시 Momentum을 반영하였기 때문에 overshooting이 여전히 발생하고 있는 것을 확인할 수 있다.