우선, 해당 포스트는 Stanford University School of Engineering의 CS231n의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
AdaGrad
AdaGrad는 SGD를 개선한 형태의 optimizer이다.
이전 iteration에서의 weight에서 learning rate $\cdot$ gradient를 빼주는 형태를 가진 SGD에서 grad_squared term을 반영해준 것인데, pseudo-code를 통해 살펴보면 조금 더 이해하기가 쉽다.
#pseudo-code for AdaGrad
grad_squared = 0
while True:
dw = compute_gradient(w)
grad_squared += dw^2
w += -learning_rate*dw/(sqrt(grad_squared)+1e-7)
즉, AdaGrad는 각 dimension마다 gradient의 historical sum of squares로 element-wise scaling을 해주는 term(grad_squared)을 추가한 것이다.(scaling term에 1e-7을 더해주는 이유는 우리가 나누는 값(scaling term)이 0이 되지 않도록 해주기 위함이다.)
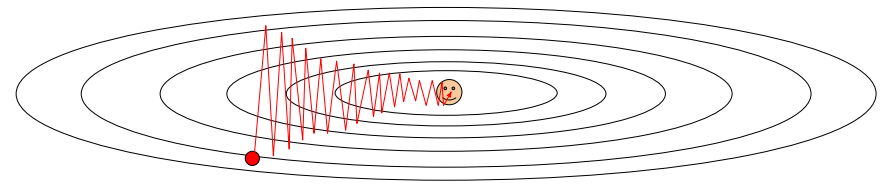
이러한 scaling term을 통하여 항상 gradient가 큰 coordinate(위 그림에서 수직축에 해당)의 경우, scaling term이 클 것이다. scaling term은 나눠지는 값이므로, 결과적으로 우리는 해당 dimension에 대한 progress를 늦출 수 있게 된다. 반면, 항상 gradient가 작은 coordinate(위 그림에서 수평축에 해당)의 경우, scaling term이 작을 것이다. 역시 나눠지는 값이므로, 결과적으로 우리는 해당 dimension에 대한 progress를 촉진(Accelerate)시킬 수 있게 된다.
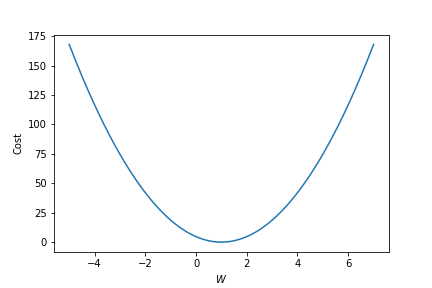
또한, gradient가 점점 작아지는 Convex case의 경우 AdaGrad의 아이디어는 상당히 좋은 성능을 보인다. 왜냐하면 iteration이 진행될 수록 grad_squared가 점점 커질 것이고, 이 때문에 매 step마다의 converge의 속도를 점점 늦출 수 있게 되어 결과적으로는 조금 더 빠르고, 정확한 converge가 가능하도록 해준다.
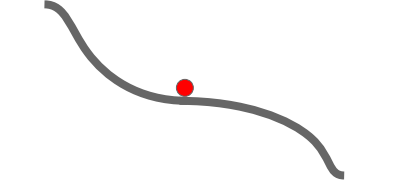
반면 Non-convex case의 경우 조금 문제가 된다. 예를들어 Saddle point의 경우를 생각해보자. Saddle point 근방에 들어올 경우, gradient가 매우 작으므로 해당 point 근방을 벗어나기가 어려워지고, 더 이상 학습이 일어나지 않게 된다는 문제점이 존재한다.
무엇보다 가장 큰 문제점은, grad_squared는 매 iteration마다 항상 더해져서 커지기만 할 뿐 작아지지 않는다는 것이다. iteration이 많이 진행되어 나누어 주는 값이 너무 커져버리면 결국 update되는 정도가 아주 작아져 버리게 되고, 자연스럽게 학습이 일어나지 않게 된다.
RMS prop
RMS prop은 AdaGrad를 다시 개선한 형태의 optimizer이며, Decay rate라는 개념을 도입한 AdaGrad optimizer라고 볼 수 있다. Decay rate은 하나의 hyper-prameter로써 보통 0.9, 0.99를 많이 사용한다.
Gradient 제곱의 합 grad_squared를 구하는 것은 AdaGrad와 동일한데, Decay rate이 있기 때문에 iteration을 거치는 과정에서 scaling term이 서서히 줄어들게(leaking) 해준다. AdaGrad의 장점은 그대로 유지하면서, Step-size가 0이되어 학습이 일어나지 않게되는 문제를 해결한 것이다.
#pseudo-code for RMS prop
grad_squared = 0
while True:
dw = compute_gradient(w)
grad_squared += decay_rate*grad_squared+(1-decay_rate)*dw^2
w += -learning_rate*dw/(sqrt(grad_squared)+1e-7)
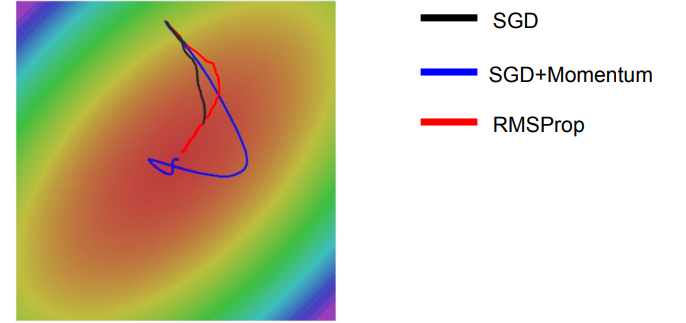
RMS prop은 학습이 조기에 종료될 수 있는 AdaGrad보다 훨씬 더 안정적이고, 빠른 속도로 학습이 끝까지 진행될 수 있도록 해준다.
Adam
#pseudo-code for Adam
first_moment = 0
second_moment = 0
while True:
dw = compute_gradient(w)
first_moment = beta1*first_moment +(1-beta1)*dw
second_moment = beta2*second_moment+(1-beta2)*dw^2
first_unbias = first_moment /(1-beta1)^t
second_unbias = second_moment/(1-beta2)^t
w += -learning_rate*first_moment/(sqrt(second_moment)+1e-7)
Adam은 앞서 살펴본 Momentum/AdaGrad/RMS prop의 장점만을 모아 하나로 결합한 형태의 optimizer이다. “first_moment” 의 경우 momentum의 개념을 도입한 부분이고, “second_moment” 의 경우 AdaGrad의 개념을 도입한 부분이다. 최종적으로 w를 update해주는 “w +=“부분의 경우, RMS prop과 상당히 유사한 형태인 것을 확인할 수 있다.
일반적으로 $\beta_1$, $\beta_2$, $\text{learning_rate}$은 기본적으로 다음 값들을 사용한다.
\[\begin{align*} \beta_1 &= 0.9\\ \beta_2 &= 0.999\\ \text{learning rate} &= 1e-3\;\;or\;\;5e-4\\ \end{align*}\]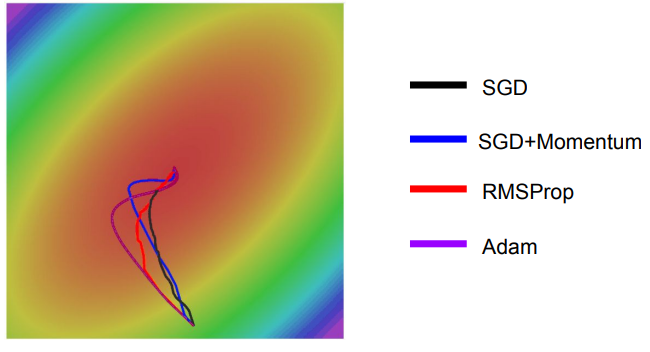
Adam optimizer의 경우 거의 대부분의 optimization 문제에서 꽤나 좋은 성능을 보이며, 그러한 이유로 많은 문제/영역에서 default optimizer로 사용되고 있다.
Comparing optimizers
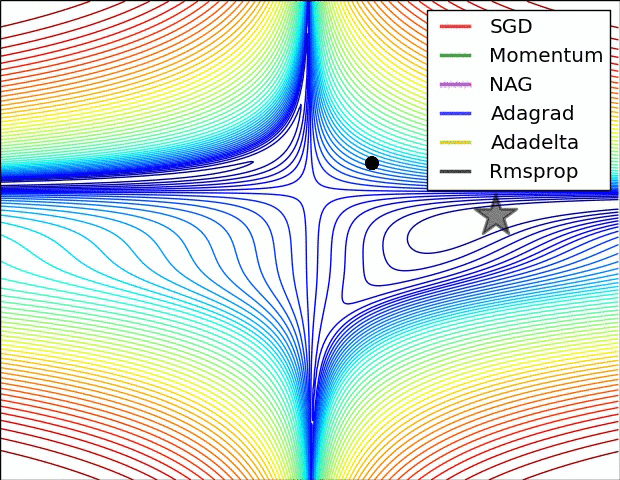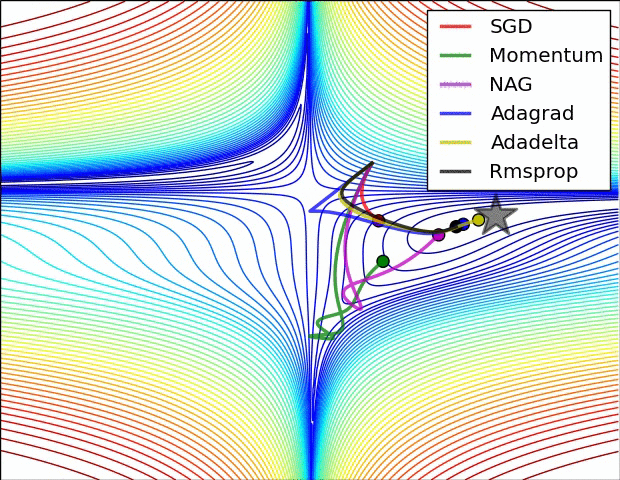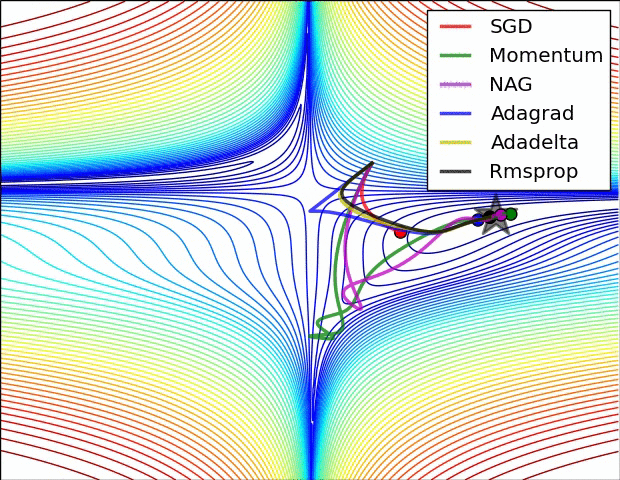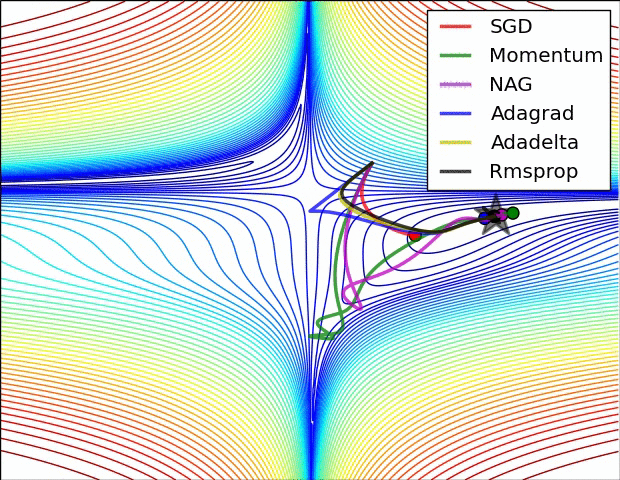
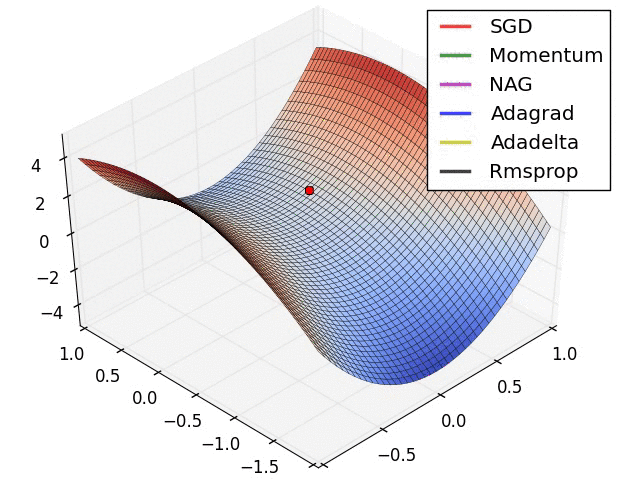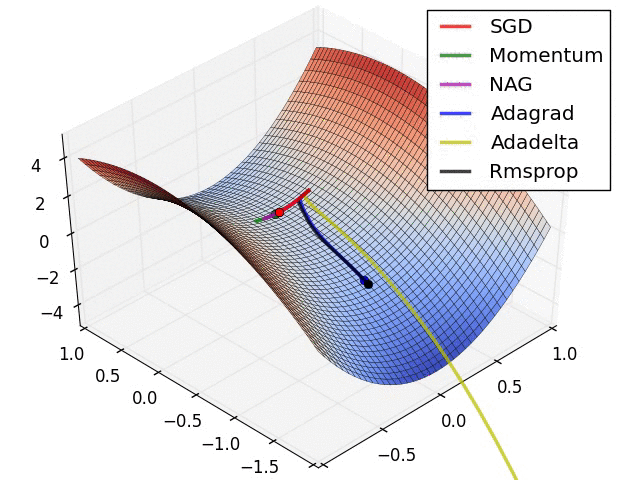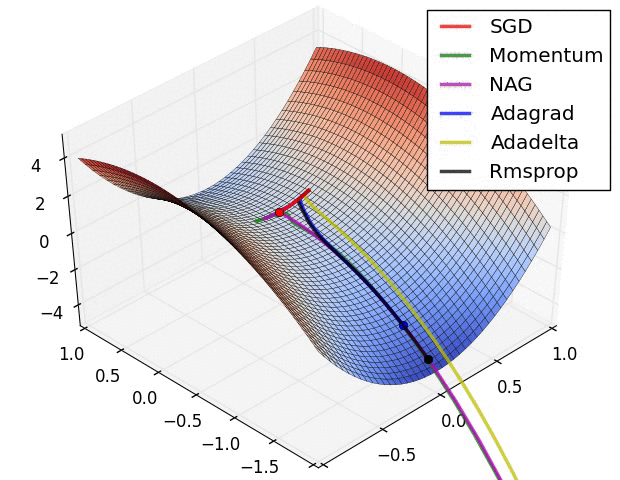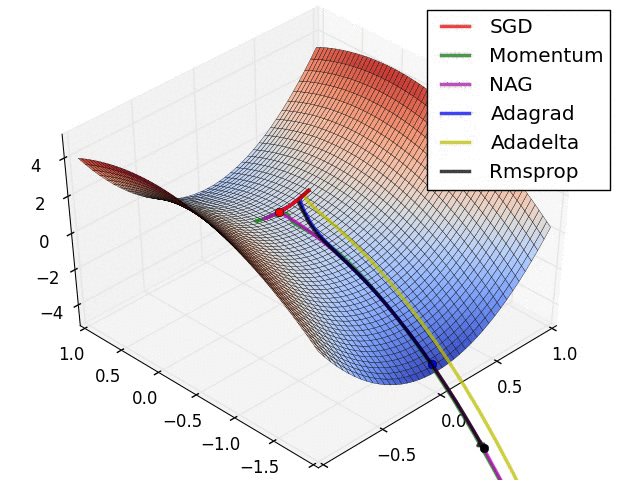
왼쪽의 그림을 통하여 각 optimizer의 performance를 시각적으로 확인할 수 있으며, Adagrad, Adadelta, RMSprop이 가장 좋은 convergence를 보여주는 것을 알 수 있다.
오른쪽의 그림은 saddle point에서의 optimization을 보여주는데, 예상하였던 것처럼 Adadelta와 RMS prop이 가장 좋은 convergence를 보여준다.
Optimization의 계보
세 Post에 걸쳐 다양한 opimization 방법에 대해 살펴보았다. 이 내용들을 한 눈에 파악할 수 있도록 잘 정리해놓은 자료를 찾아서 공유하고자 한다. 아래 그림은 하용호님의 Slide에서 가져온 자료이다.
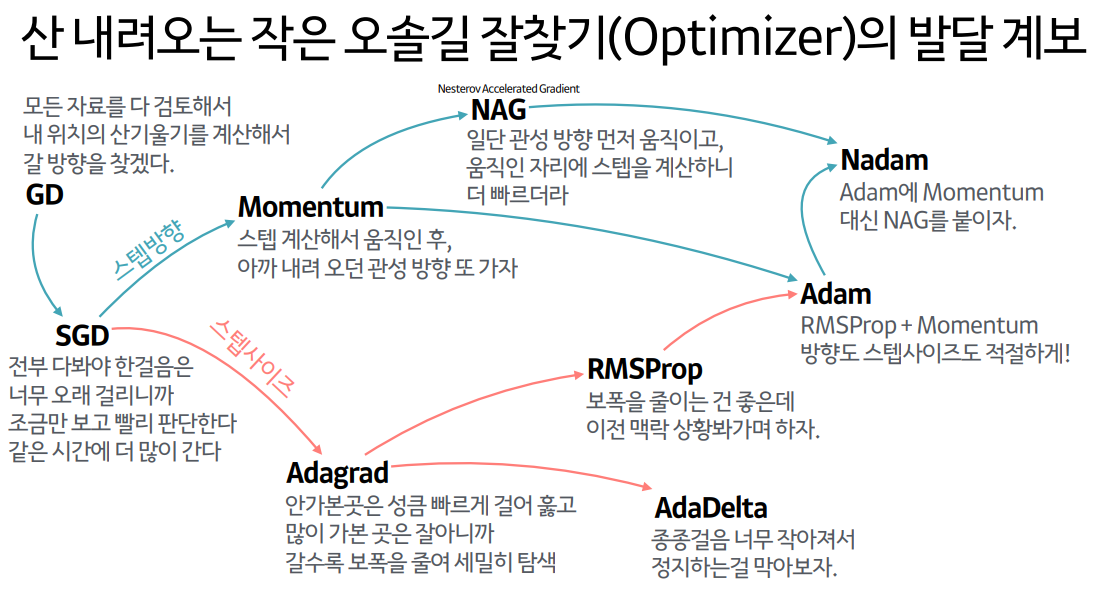
Reference
CS231n: Lecture 7, Training Neural Networks II