우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 모두를 위한 딥러닝 시즌2의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
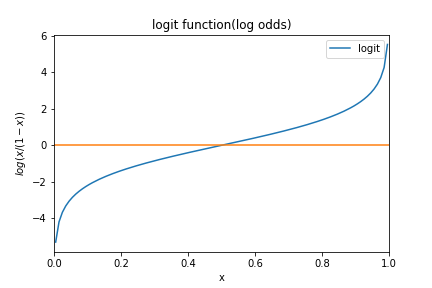
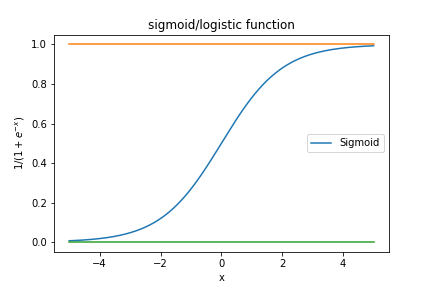
odds, logit, logistic, sigmoid
우리는 logistic regression을 다룰 때 마다 항상 odds, logit, logistic, sigmoid라는 단어들과 마주치게 된다. 모델의 형태를 어떻게 정리하느냐에 따라 부르는 이름이 달라지기도 하고, 학문의 분야에 따라 같은 함수에 다른 이름을 붙여주기도 하면서 이러한 단어들이 생겨나게 되었다. 헷갈릴 수도 있겠지만, 하나하나씩 차근차근 정리해보면 다음과 같다.
\[\begin{align*} odds(x) &= {x \over 1-x}\\ logit(x) &= log(odds(x)) \\&= log({x \over 1-x})\\ sigmoid(x) &= logistic(x) = logit^{-1}(x)\\ &= {1 \over 1+exp(-x)} \\&= {exp(x) \over exp(x)+1} \end{align*}\]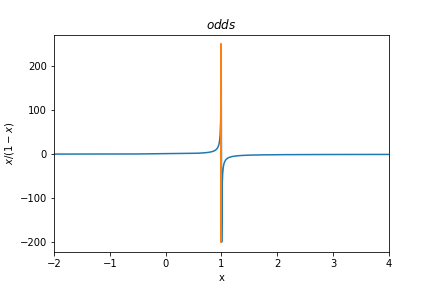
Logistic Regression
Generalized Linear model(GLM) 포스트에서 살펴보았던 Logistic regression에 대하여 다시 살펴보도록 하자. Logistic regression의 경우 link function이 다음과 같은 형태를 가진다.
\[\begin{align*} E[y_i] &= \mu_i\\ g(\mu_i) &= logit(\mu_i) = {\mu_i \over 1-\mu_i} = x_i' \beta \end{align*}\]이를 $\mu_i$에 대해 다시 정리하면 우리가 잘 알고있는 로지스틱 함수가 된다.
\[\mu_i = logistic(x_i' \beta) = \frac 1 {1+e^{-x_i' \beta}}\]logistic 함수의 결과 값은 0에서 1사이에 위치하게 되는데, 우리는 이 값을 $x$가 주어졌을 때의 $y=1$일 조건부 확률로 해석할 수 있다. 즉, 주어진 $x$에서 logistic function의 값이 cut-off를 넘을 경우, 해당 data에 해당하는 $y$의 값이 1일 것으로 예측할 수 있게 되는 것이다.
MLE of Logistic Regression
Binary classification 문제에 대하여 생각해보자. $p$를 다음과 같이 정의하도록 한다.
\[p_i = Pr(y_i=1 \vert x_i) = logistic(x_i'\beta) = \frac 1 {1+e^{-x_i'\beta}}\]여기서 $y$는 1과 0의 두 값을 취하고, $p$는 $y$가 1일 확률이므로 우리는 $y$에 대하여 Bernoulli 분포를 가정할 수 있다.
\[Y_i \sim Bernoulli(p_i) = Bernoulli(\frac 1 {1+e^{-x_i'\beta}})\] \[Pr(Y_i=y_i) = {p_i}^{y_i} (1-{p_i})^{1-y_i} = \left \lbrack {\frac 1 {1+e^{-x_i'\beta}}} \right \rbrack^{y_i} \left \lbrack1-{\frac 1 {1+e^{-x_i'\beta}}}\right \rbrack^{1-y_i}\]이 때 $p$의 log-likelihood를 구해보면 다음과 같다.
\[\begin{align*} L(p \vert y) &= \prod_{i=1}^n f(y_i \vert p_i) \\ &= \prod_{i=1}^n Pr(Y_i = y_i \vert p_i)\\ l(p \vert y) &= log(L(p \vert y)) \\ &=\sum_{i=1}^n log(Pr(Y_i = y_i \vert p_i))\\ &=\sum_{i=1}^n log({p_i}^{y_i} (1-{p_i})^{1-y_i})\\ &=\sum_{i=1}^n \left \lbrack y_i log(p_i) + (1-y_i)log(1-p_i) \right \rbrack\\ \end{align*}\]따라서, $\beta$에 대한 log-likelihood는 다음과 같다.
\[\begin{align*} L(\beta \vert y) &= \prod_{i=1}^n f(y_i \vert x_i, \beta)\\ &= \prod_{i=1}^n Pr(Y_i = y_i \vert x_i, \beta)\\ l(\beta \vert y) &= log(L(\beta \vert y)) \\ &=\sum_{i=1}^n log(Pr(Y_i = y_i \vert x_i, \beta))\\ &=\sum_{i=1}^n log \left \lbrack \left \lbrack {\frac 1 {1+e^{-x_i'\beta}}} \right \rbrack^{y_i} \left \lbrack1-{\frac 1 {1+e^{-x_i'\beta}}}\right \rbrack^{1-y_i} \right \rbrack\\ &=\sum_{i=1}^n \left \lbrack y_i log \left \lbrack \frac 1 {1+e^{-x_i'\beta}} \right \rbrack + (1-y_i)log\left \lbrack1-\frac 1 {1+e^{-x_i'\beta}} \right \rbrack \right \rbrack \end{align*}\]위와 같이 log-liklihood $l(\beta \vert y)$를 성공적으로 구하였다. 일반적으로 우리는 log-likelihood를 구한 후에 이를 최대화하는 $\beta$를 찾게 된다.
하지만 로지스틱 회귀의 경우 해당 식에 대한 해답이 closed-form으로 존재하지 않는다. 따라서 numerical한 optimization을 통하여 구할 수 밖에 없다.
Example
학생 6명의 영어/수학 공부 시간에 대한 정보와 시험 합격 여부에 대한 데이터를 가지고 있다고 가정하자.
A학생은 영어를 1시간, 수학을 2시간 공부하였으며, 결국 시험에 합격하지 못하였다. B학생은 영어를 2시간, 수학을 3시간 공부하였으며, 결국 시험에 합격하지 못하였다. C학생은 영어를 3시간, 수학을 1시간 공부하였으며, 결국 시험에 합격하지 못하였다. D학생은 영어를 4시간, 수학을 3시간 공부하였으며, 결국 시험에 합격하였다. E학생은 영어를 5시간, 수학을 3시간 공부하였으며, 결국 시험에 합격하였다. F학생은 영어를 6시간, 수학을 2시간 공부하였으며, 결국 시험에 합격하였다.
이 때 우리는 영어/수학 공부 시간과 시험 합격 여부 간의 관계에 대하여 모델링을 하려고 한다. 이 경우 시험 합격/불합격을 예측하는 문제로 볼 수 있으므로, 다음과 같이 Logistic Regression 모형을 사용할 수 있다.
단 주의할 점은 optimization을 통하여 cost를 최소화하는 문제를 풀고 있으므로 최소화시키는 대상이 log-likelihood가 아닌, negative log-likelihood라는 점이다. 우리는 이러한 loss 함수를 Binary Cross Entropy loss 라고 부른다.
Source code 1: naive version
import torch
# For reproducibility
torch.manual_seed(1)
# dataset
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
# weight initialization
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer
optimizer = torch.optim.SGD([W, b], lr=1)
n_epochs = 1000
for epoch in range(n_epochs + 1):
# hypothesis: sigmoid
hypothesis = 1/(1+torch.exp(-(x_train.matmul(W)+b)))
# cost: Binary Cross Entropy loss
cost = -(y_train*torch.log(hypothesis)+(1-y_train)*torch.log(1-hypothesis)).mean()
# updating weights
optimizer.zero_grad()
cost.backward()
optimizer.step()
# print
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, n_epochs, cost.item()
))
Source code 2: Using torch.sigmoid, torch.nn.functional.binary_cross_entropy
import torch
# For reproducibility
torch.manual_seed(1)
# dataset
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
# weight initialization
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer
optimizer = torch.optim.SGD([W, b], lr=1)
n_epochs = 1000
for epoch in range(n_epochs + 1):
# hypothesis: sigmoid
hypothesis = torch.sigmoid(x_train.matmul(W)+b)
# cost: Binary Cross Entropy loss
cost = torch.nn.functional.binary_cross_entropy(hypothesis, y_train)
# updating weights
optimizer.zero_grad()
cost.backward()
optimizer.step()
# print
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, n_epochs, cost.item()
))
Source code 3: Using High level API
import torch
torch.manual_seed(1)
class BinaryClassifier(torch.nn.Module):
def __init__(self):
super().__init__()
self.linear = torch.nn.Linear(2, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
return self.sigmoid(self.linear(x))
# dataset
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
# model
model = BinaryClassifier()
# optimizer
optimizer = torch.optim.SGD(model.parameters(), lr=1)
n_epochs = 1000
for epoch in range(n_epochs + 1):
# hypothesis
hypothesis = model(x_train)
# cost
cost = torch.nn.functional.binary_cross_entropy(hypothesis, y_train)
# updating weights
optimizer.zero_grad()
cost.backward()
optimizer.step()
# print
if epoch % 10 == 0:
prediction = hypothesis >= torch.FloatTensor([0.5])
correct_prediction = prediction.float() == y_train
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format(
epoch, n_epochs, cost.item(), accuracy * 100,
))
Reference
CS231n, Stanford University School of Engineering