Perceptron

우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 모두를 위한 딥러닝 시즌2의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.

Perceptron

Perceptron은 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘이이며, Frank Rosenblatt가 1957년에 제안한 초기 형태의 인공 신경망이다.

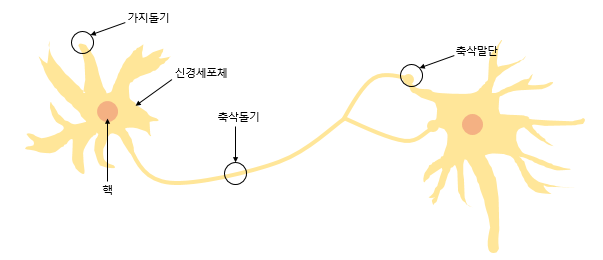
퍼셉트론은 실제 뇌를 구성하는 신경 세포 뉴런의 동작과 유사한데, 신경 세포 뉴런의 그림을 먼저 보도록 하자. 뉴런은 가지돌기에서 신호를 받아들이고, 이 신호가 일정치 이상의 크기를 가지면 축삭돌기를 통해서 신호를 전달한다.

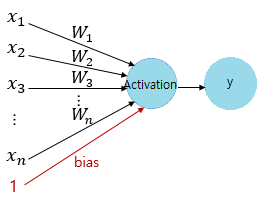
퍼셉트론의 구조도 이와 비슷하다. 그림에서의 원은 뉴런, $W$는 신호를 전달하는 축삭돌기의 역할을 하게 된다. 각 뉴런에서 보내지는 입력값 $x$를 가중치 $W$에 곱해주고, 이 값을 Activation 함수를 통과시켜 뉴런 $y$로 전달해주는 것이다.

그런데 이 구조를 어디서 많이 보지 않았는가? 이 Activation 함수에 $Sigmoid$ 함수를 사용하면 Logistic Regression이 되고, $Softmax$ 함수를 사용하면 Softmax classifier(Multiclass Logistic Regression) 모형이 된다. 즉, 하나의 로지스틱 회귀(혹은 Softmax Classifier) 모형은 Perceptron의 special case라고 볼 수 있는 것이다.

이러한 하나의 perceptron은 Neural Networks의 전체적인 구조 안에서 하나의 뉴런 역할을 하게 된다.

Single layer perceptron

앞서 살펴본 구조의 perceptron을 단층(Single layer) perceptron이라고 한다. 단층 퍼셉트론은 $x$값을 내보내는 input layer와, 값을 받아 출력하는 output layer의 총 2개의 layer로만 이루어진 형태의 perceptron을 의미한다.

Single layer perceptron을 활용하면 AND gate와 OR gate를 쉽게 구현할 수 있다.

AND gate

$x_1$	$x_2$	$y$
0	0	0
0	1	0
1	0	0
1	1	1

AND 게이트는 두 개의 입력 값 $x_1$과 $x_2$가 모두 1인 경우에만 출력값 $y$가 1이 나오는 구조를 가지고 있다. 표로 보면 잘 이해가 안될 수도 있는데, 다음 그림을 보면 이해가 훨씬 쉽다.

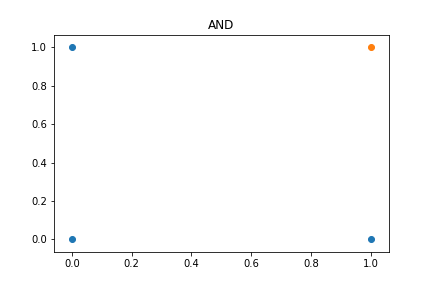
그림에서 볼 수 있듯이, (0,0), (0,1), (1,0)의 경우 class 0이며, (1,1)의 경우에만 class 1에 속해 있는 것을 확인할 수 있다.

이 AND 게이트를 $Sigmoid$함수를 사용한 단층 perceptron으로 구현해보면 다음과 같다.(이 경우 $Sigmoid$함수를 Activation 함수로 사용하였으므로, 이 perceptron은 logistic regression과 같다.)

import torch

# setting device
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# dataset
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [0], [0], [1]]).to(device)

# model
linear = torch.nn.Linear(2, 1, bias=True)
sigmoid = torch.nn.Sigmoid()
model = torch.nn.Sequential(linear, sigmoid).to(device)

# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)

for step in range(1001):
    # hypothesis
    hypothesis = model(X)

    # cost/loss function
    cost = criterion(hypothesis, Y)

    # updating weights
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    #print
    if step % 100 == 0:
        print(step, cost.item())

다음과 같이 testset으로 적합시킨 perceptron을 평가해보면, 100%의 Accuracy를 보이는 것을 확인할 수 있다.

# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

OR gate

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	1

OR 게이트는 두 개의 입력 값 $x_1$과 $x_2$가 모두 0인 경우에만 출력값 $y$가 0이고, 나머지의 경우에는 1이 나오는 구조를 가지고 있다. 역시 그림을 보면 이해가 훨씬 쉽다.

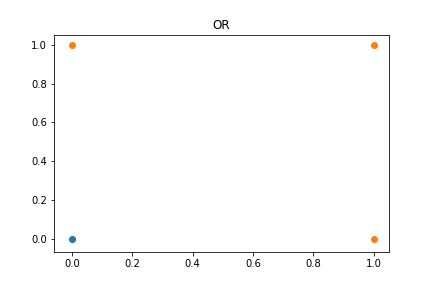
그림에서 볼 수 있듯이, (0,1), (1,0), (1,1)의 경우 class 1이며, (0,0)의 경우에만 class 0에 속해 있는 것을 확인할 수 있다.

이 OR 게이트를 $Sigmoid$함수를 사용한 단층 perceptron으로 구현할 수 있고, 역시 Test해보면 Accuracy 100%의 단층 perceptron을 구현할 수 있다는 사실을 알 수 있다.

XOR gate

앞서 AND gate와 OR gate는 단층 Perceptron으로 쉽게 구현할 수 있다는 것을 확인하였다.

하지만 XOR gate의 경우 이야기가 조금 달라진다. XOR gate는 다음과 같다.

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	0

XOR 게이트는 두 개의 입력 값 $x_1$과 $x_2$가 모두 0이거나, 모두 1인 경우에만 출력값 $y$가 0이고, 나머지의 경우에는 1이 나오는 구조를 가지고 있다. 역시 그림을 보면 이해가 훨씬 쉽다.

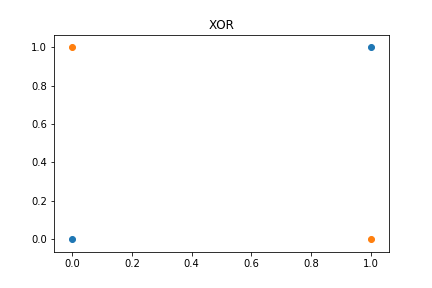
이 문제는 단층 perceptron으로 풀 수 없는데, 그 이유는 두 집단을 구분지을 수 있는 하나의 linear 함수를 찾을 수 없기 때문이다. 간단하게 위 그림에서 하나의 직선을 그려서 두 집단을 구분할 수 있는지 생각해보자. 불가능할 것이다.

아래와 같이 single layer perceptron을 적합시켜 보아도, prediction이 잘 되지 않아 정확도가 50%밖에 되지 않는 것을 확인할 수 있다.

import torch

# setting device
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# dataset
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)

# model
linear = torch.nn.Linear(2, 1, bias=True)
sigmoid = torch.nn.Sigmoid()
model = torch.nn.Sequential(linear, sigmoid).to(device)

# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=1)

for step in range(1001):
    # hypothesis
    hypothesis = model(X)

    # cost/loss function
    cost = criterion(hypothesis, Y)

    # updating weights
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    #print
    if step % 100 == 0:
        print(step, cost.item())

# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

Reference

CS231n, Stanford University School of Engineering

모두를 위한 딥러닝 시즌2

PyTorch로 시작하는 딥 러닝 입문