우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 모두를 위한 딥러닝 시즌2의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
Activation function
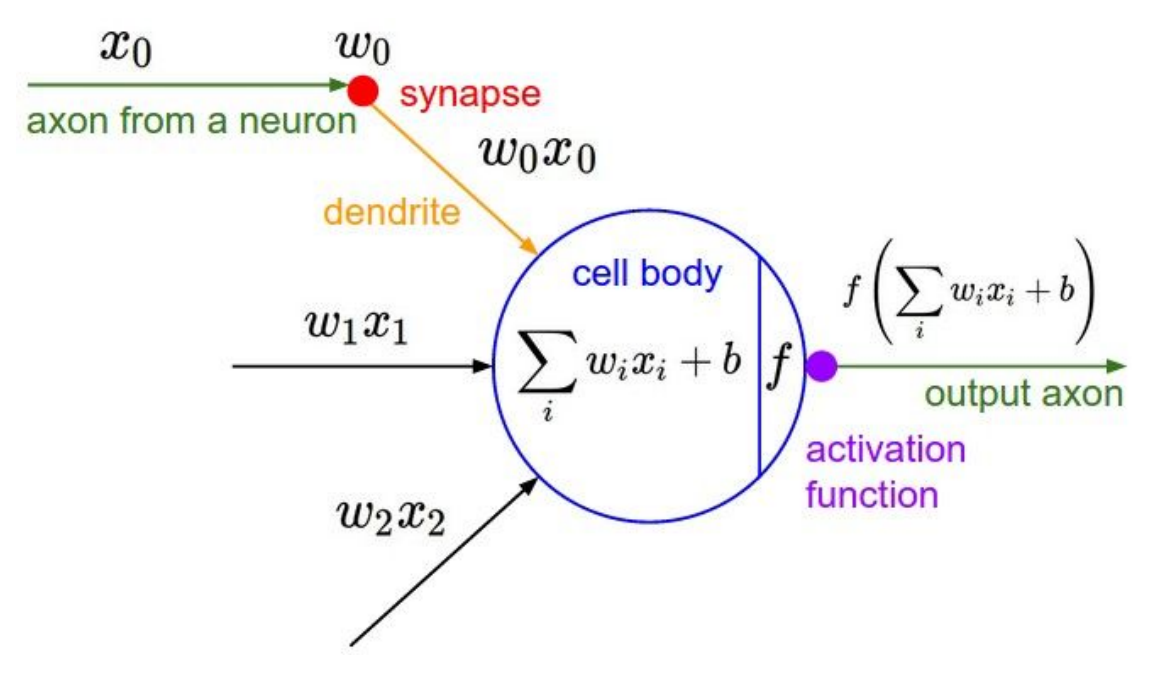
일반적인 Neural Networks는 $\sum_i W_iX_i$를 계산한 후에 Sigmoid와 같은 함수 $f$를 통하여 transformation해주는 작업을 각 layer마다 반복하게 된다. 이러한 transformation function $f$를 우리는 Activation Function 이라고 한다.
이번 포스트에서는 Neural Networks에서 Activation function으로 Sigmoid function을 사용하였을 때의 단점을 살펴보고, 이를 보완하여 고안된 다양한 Activation function을 살펴보도록 하겠다.
Sigmoid
\[\sigma(x) = \frac 1 {1+e^{-x}}\]앞서 우리는 여기에서 Sigmoid 함수를 Activation함수로 사용한 Softmax classifier를 통하여 MNIST dataset classification을 해보았다.
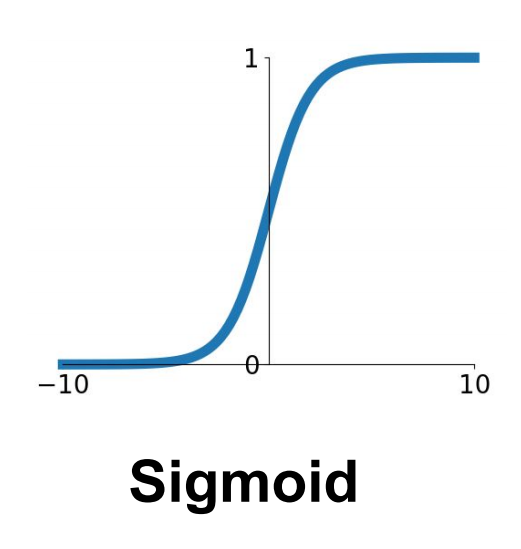
Sigmoid 함수의 경우 0부터 1까지 범위의 값을 가지며, 통계학에서 아주 많이 사용되는 함수이다.
하지만 Sigmoid 함수의 경우 Neural Networks에서 Activation 함수로 사용하기에는 매우 부적절한 함수이며, 크게 3가지 이유가 존재한다.
(1) Vanishing Gradient
Sigmoid function을 Activation function으로 가지는 경우, $\partial \sigma \over \partial w$를 계산해야 하며, 이는 Back propagation을 통하여 ${\partial \sigma \over \partial w} = {\partial \sigma \over \partial X} \cdot {\partial X \over \partial w}$와 같이 계산할 수 있다.
여기서 문제가 되는 부분은 Sigmoid 함수에 대한 미분 값인 ${\partial \sigma \over \partial X}$의 크기에 대한 문제이다. 다음 그림을 살펴보자.
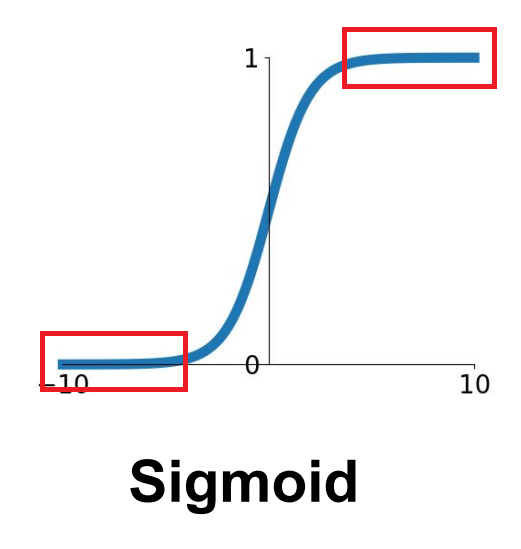
위 그림에서 빨간 박스에 해당하는 부분은 Gradient가 거의 0에 가까운 아주 작은 숫자를 가진다. 즉, $X$가 0보다 꽤 작거나, 클 경우 ${\partial \sigma \over \partial X} \approx 0$가 된다. 이렇게 Sigmoid 함수에서 Gradient가 거의 0에 가까운 부분을 Saturated Regime 이라고 부른다.
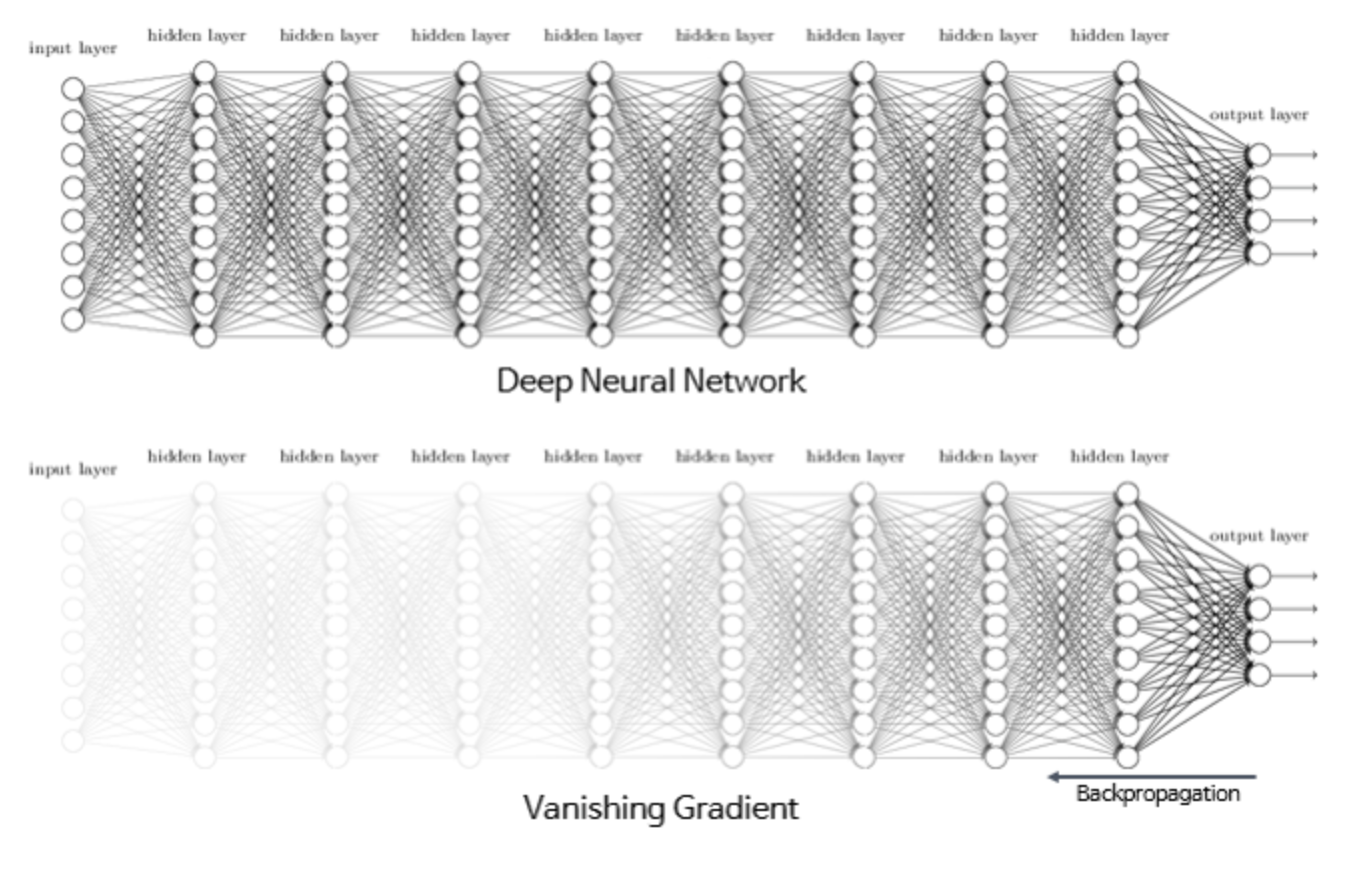
이는 Multi layer perceptron에서 큰 문제가 된다. layer가 많을 경우 최종적인 Global Gradient를 구하기 위하여 local Gradient를 상당히 많이 곱해주게 되는데(Back propagation), 이 과정에서 0에 가까운 값들을 계속 곱해주게 되는 것이다. 이로 인하여 앞단에 위치한 layer일 수록 Gradient 값들을 제대로 구하지 못하고 거의 0에 수렴해버리는 문제가 발생하며, 이로 인하여 Weight들이 제대로 update되지 못하게 된다. 이러한 현상을 Vanishing Gradient 라고 한다.
(2) Not zero-centered
Sigmoid 함수의 경우 output 값이 0.5를 중심으로 하며, 0과 1사이에 위치해 있다. 하지만 Neural Networks의 경우 이러한 구조의 Activation 함수는 좋은 성능을 보이지 못한다.
Multi layer를 가정하여 어떤 layer는 앞단의 sigmoid로부터의 output을 받아 input $x$로 사용한다고 하자. Sigmoid 함수의 결과 값은 항상 양수 이므로, 이 경우 $x$는 항상 양수이다. 이러한 양수의 $x$를 input으로 받아 linear combination $F$을 계산하고($F = \sum_{i=1}^n (w_ix_i+b$), 여기에 activation function으로 sigmoid를 주어 결과값 $L(F) = L(\sum_{i=1}^n w_ix_i+b)$를 만들어 낸다고 가정하자. 이 구조를 정리해보면 다음과 같다.
\[\text{output from last $n$ sigmoids $\sigma_{1,prev}, \cdots, \sigma_{n,prev}$}\\ x_1, x_2, \cdots, x_n>0\\ \downarrow\\ \text{$F = \sum_{i=1}^n w_ix_i+b$ is used as a new input of a next step's sigmoid}\\ F = \sum_{i=1}^n w_ix_i+b\\ \downarrow\\ \text{final output of a sigmoid, } L\\ L = L(F) =L(\sum_{i=1}^n w_ix_i+b) = {1 \over 1+exp(-\sum_{i=1}^n w_ix_i+b)}\\\]우선, $\frac {\partial F} {\partial w_i}$ 값의 부호에 대해 생각해보자. $\frac {\partial F} {\partial w_i}$는 다음과 같이 구할 수 있다.
\[\begin{align*} \frac {\partial F} {\partial w_1} &= x_1 > 0\\ \frac {\partial F} {\partial w_2} &= x_2 > 0\\ \vdots \;\;\; &= \; \vdots \\ \frac {\partial F} {\partial w_n} &= x_n > 0\\ \end{align*}\]$\frac {\partial F} {\partial w_i}$의 값은 항상 $x_i$와 같다. 그런데 사실 모든 $x_i$는 이전 layer에서의 sigmoid 함수의 결과값이므로 양수이다. 즉, $\frac {\partial F} {\partial w_i}$는 항상 $\frac {\partial F} {\partial w_i}>0$ 임을 알 수 있다.
이제 Final output $L = {1 \over 1+exp(-\sum_{i=1}^n w_ix_i+b)}$를 각 $w_i$로 미분한 값들(Global Gradient)에 대해 생각해보자. $\frac {\partial L} {\partial w_1}$, $\frac {\partial L} {\partial w_2}$, $\cdots$, $\frac {\partial L} {\partial w_n}$을 구해보면 다음과 같다.
\[\begin{align*} \frac {\partial L} {\partial w_1} &= \frac {\partial L} {\partial F} \frac {\partial F} {\partial w_1} \\ \frac {\partial L} {\partial w_2} &= \frac {\partial L} {\partial F} \frac {\partial F} {\partial w_2} \\ \vdots\;\;\; &= \;\;\;\;\;\;\vdots\\ \frac {\partial L} {\partial w_n} &= \frac {\partial L} {\partial F} \frac {\partial F} {\partial w_n} \\ \end{align*}\]아까 살펴보았듯이, $\frac {\partial F} {\partial w_i}$는 모든 $i$에 대하여 양수라는 것을 알고 있다.
또한, $\frac {\partial L} {\partial F}$의 경우 $\frac {\partial L} {\partial F} = (1-L(F))L(F)$로 계산되며, 양수와 음수의 값 모두가 될 수 있다.
이 두 사실을 종합하면, 다음과 같이 $\frac {\partial L} {\partial w_i}$의 부호와 $\frac {\partial L} {\partial F}$의 부호가 같다는 사실을 이끌어낼 수 있다.
\[\begin{align*} sign(\frac {\partial L} {\partial w_1}) &= sign(\frac {\partial L} {\partial F})\\ sign(\frac {\partial L} {\partial w_2}) &= sign(\frac {\partial L} {\partial F})\\ \vdots\;\;\; &= \;\;\;\;\;\;\vdots\\ sign(\frac {\partial L} {\partial w_n}) &= sign(\frac {\partial L} {\partial F})\\ \end{align*}\]그런데 여기서 우변이 모두 같으므로, 다음과 같이 $L$에 대한 모든 $w_i$의 미분 값의 부호가 같다는 사실을 알 수 있다. 즉, $\frac {\partial L} {\partial F}$가 양수/음수라면 모든 $\frac {\partial L} {\partial w_i}$가 양수/음수로 같은 부호를 가지는 것이다.
\[\begin{align*} sign(\frac {\partial L} {\partial w_1}) = sign(\frac {\partial L} {\partial w_2}) = \cdots = sign(\frac {\partial L} {\partial w_n}) = sign(\frac {\partial L} {\partial F})\\ \end{align*}\]이는 training의 성능 저하에 꽤나 큰 영향을 미치는데, 다음 그림을 살펴보자.
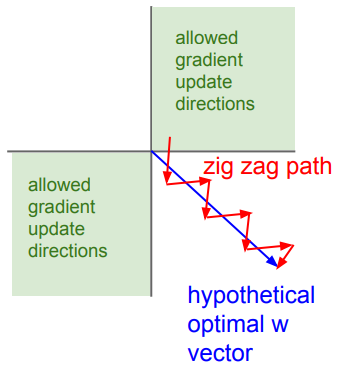
시각적으로 쉽게 설명하기 위하여 2개의 weight $w_1$, $w_2$만 존재한다고 가정하자. 이 때 가로축은 $w_1$, 세로축은 $w_2$에 대한 축이며, 파란색 벡터를 weight $(w_1, w_2)$의 optimal한 학습 방향이라고 하자.
만약, 모든 weights($w_1$과 $w_2$)에 대한 gradient의 부호 값이 같다면, 학습되는 방향 또한 같은 방향일 수 밖에 없다. 즉, 그림에서 연두색으로 표시된 방향으로만 학습이 되는 것이다.
결과적으로 오른쪽 아래의 방향으로 학습되는 과정에서 $\rightarrow$ 방향과 $\downarrow$ 방향으로 번갈아 가며 학습되게 되고, 그림에서 빨간 직선의 과정을 거쳐 같이 학습이 이루어지게 된다. 즉, 결과적으로 학습 과정이 매우 느려지고, 효율적이지 못하게 되는 것이다.
(3) Computationally expensive
Sigmoid 함수는 다음과 같은 형태를 가진다.
\[\sigma(x) = \frac 1 {1+e^{-x}}\]사실 Sigmoid에 들어가 있는 Exponential 함수 $exp$는 computing 시에 비교적 연산히 오래걸린다는 단점이 존재한다. Neural Networks에서 Sigmoid를 사용할 경우 매우 많은 Activation 함수값을 계산해야 하므로, Activation fucntion으로 Sigmoid 함수를 사용할 경우 Computationally expensive하다는 점이 문제가 될 수 있다.
세 가지 문제 중, 앞의 두 가지 문제 Vanishing Gradient 와 Not zero centered 는 큰 문제로 부각되지만, 계산상의 비효율성에 대한 문제는 사실 큰 문제가 되지는 않는다.
Reference
CS231n, Stanford University School of Engineering