우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료를 기본으로 하여 정리한 내용임을 밝힙니다.



ILSVRC’15

이번 포스트에서 살펴볼 모델은 ILSVRC’15의 Classification task에서 1등을 차지한 ResNet을 살펴보도록 하겠다.



ResNet(2015)

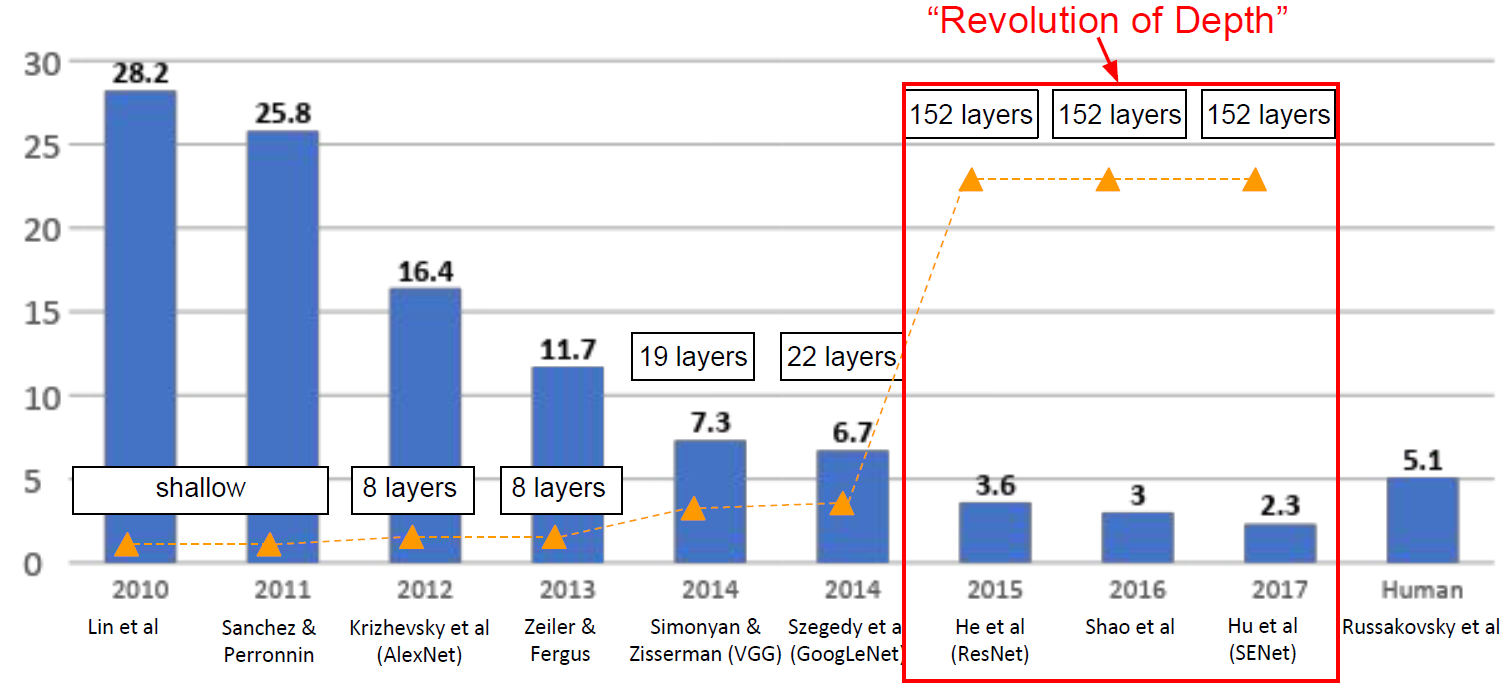
paper: He et al.(2015), Deep Residual Learning for Image Recognition


Deeper networks

ILSVRC’15부터 ILSVRC’17까지는 Revolution of Depth 라고 표현할 수 있을 정도로 모델의 Depth에 획기적인 변화가 찾아온다. 위 그림에서 확인할 수 있듯이, 이전의 ILSVRC 우승 모델들과는 비교가 안 될 정도로 깊은 구조를 가지는 모델들이 우승을 차지하게 된 것이다.

ResNet에서 layer의 깊이는 152-layer까지 깊어졌으며, 2015년의 모든 classification과 detection 대회에서 우승을 차지하였다. 즉, 모든 방면에서 이전의 모델들보다 훨씬 더 뛰어난 모델이 등장하게 된 것이다.


Errors in Deeper networks

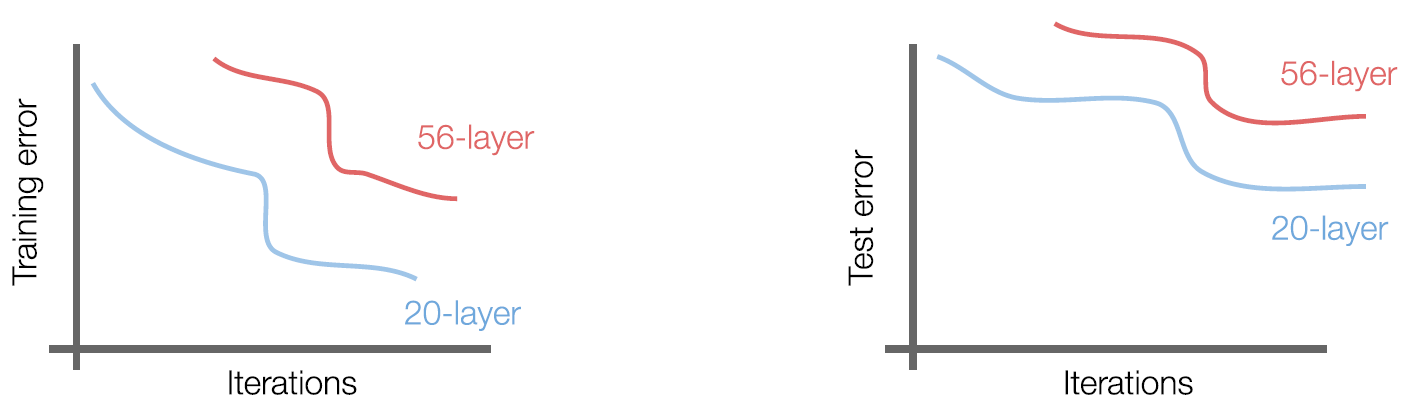
얼핏 생각하면 기본적으로 Layer의 수가 많아지면 classification 성능이 더 좋아져야만 할 것 같지만 사실 꼭 그렇지만은 않다. 위 그림은 conv-pooling을 반복하는 일반적인 CNN에 대하여 training error와 test error를 20-layer/56-layer의 depth에 대하여 비교한 그림이다.

그림에서 확인할 수 있듯이, ResNet이 아닌 평범한 CNN 모델들의 경우 Layer가 많아짐에 따라 Test Error가 커지는 결과를 보인다. 즉, 결과적으로 깊은 구조의 CNN(56-layer)이 얕은 구조의 CNN(20-layer)보다 더 좋은 performance를 보이지 못하는 것이다.

더욱더 눈여겨보아야 할 부분은 training error이다. 왼쪽 그림에서 training error를 살펴볼 수 있는데, training error 또한 깊은 CNN에서 더 높다는 것을 확인할 수 있다. 이는 더 깊은 CNN에서 성능이 좋지 않은 것은 overfitting 때문이 아니라는 것을 알 수 있는 대목이다.


Why?

망이 깊어지면 발생하는 문제에 대한 근본적인 원인들 중에서 Vanishing/Exploding Gradient 이 가장 큰 원인으로 손꼽힌다. 이는 Gradient가 너무 작아지거나, 너무 커져버려서 더 이상 적절히 학습이 진행되지 않는 것을 뜻한다. 물론 Batch normalization 등을 통하여 이 문제를 어느정도 해결할 수는 있지만, 망이 너무 깊어질 경우 이 마저도 해결이 쉽지 않다.

ResNet을 만든 He는 깊은 구조의 CNN의 performance가 좋지 않은 것은 해당 문제와 같은 이유로 깊은 구조의 model에서는 optimization이 힘들기 때문이지 않을까 라는 생각에 도달하게 된다.


Skip Connection: Residual Learning Framework


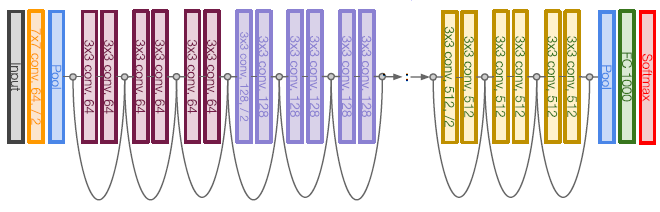
ResNet은 skip connection(Residual Block) 이라는 개념을 도입하여 이 문제를 해결한다.

기존의 CNN(Plain layers)에서는 Forward pass시에 CONV-ReLU-CONV과 같은 구조의 레이어를 쌓아 계산하였다면, ResNet의 경우(Residual block) CONV-ReLU-CONV를 계산한 값에 input X를 더해주어 해당 layer의 output으로 계산해준다. 사실 아주 간단한 아이디어이며 전혀 복잡하지 않아 보이는데, 단순히 layer의 output에 input을 더해주는게 무슨 의미가 있는 것일까?

기존의 CNN에서는 input $X$가 들어왔을 때, output $H(X)$가 올바르게 계산될 수 있도록 함수 $H$를 학습한다. layer의 깊이가 깊지 않을 때에는 큰 문제가 되지 않지만, layer의 깊이가 깊어졌을 때에는 optimization이 쉽지 않아 적절한 함수 $H$의 학습에 어려움이 따른다.


\[\begin{align*} H(X) &= F(X) + X\\ &= \text{Residual} + \text{Identity} \end{align*}\]

반면, Residual mapping을 사용할 경우 문제 해결이 훨씬 쉬워진다. $X \rightarrow H(X)$를 학습하는 것이 아닌 $X \rightarrow X+F(X)$, 즉 $F$만 학습하는 것으로 문제를 해결한다.

쉽게 설명하면 복잡한 함수 $H$를 학습하는 것보다, 비교적 간단한 함수 $F$를 학습하는 것이 훨씬 쉽기 때기 때문에 결과적으로 깊은 layer에서도 $F$에 대한 학습이 잘 이루어 지게 된다.

ResNet의 경우 이러한 문제를 해결하게 되고, ILSVRC’14까지 선보였던 여느 다른 모델들보다 기하급수적으로 많은 수의 Layer를 사용하여 3.6% top5 error rate를 달성하게 된다.



Reference

CS231n

He et al.(2015), Deep Residual Learning for Image Recognition