GAN(Generative Adversarial Networks)

우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 고려대학교 최윤제 연구원님의 Naver D2(Naver Engineering) 발표 자료를 기본으로 하여 정리한 내용임을 밝힙니다.

Generative Adversarial Networks

Generative Adversarial Networks 는 2014년 NIPS에 발표된 논문으로써 생성자(Generator)와 구분자(Discirimiator)의 두 네트워크를 적대적으로 학습시키는 비지도 학습 기반의 생성모델(Unsupervised Generative model)이다.

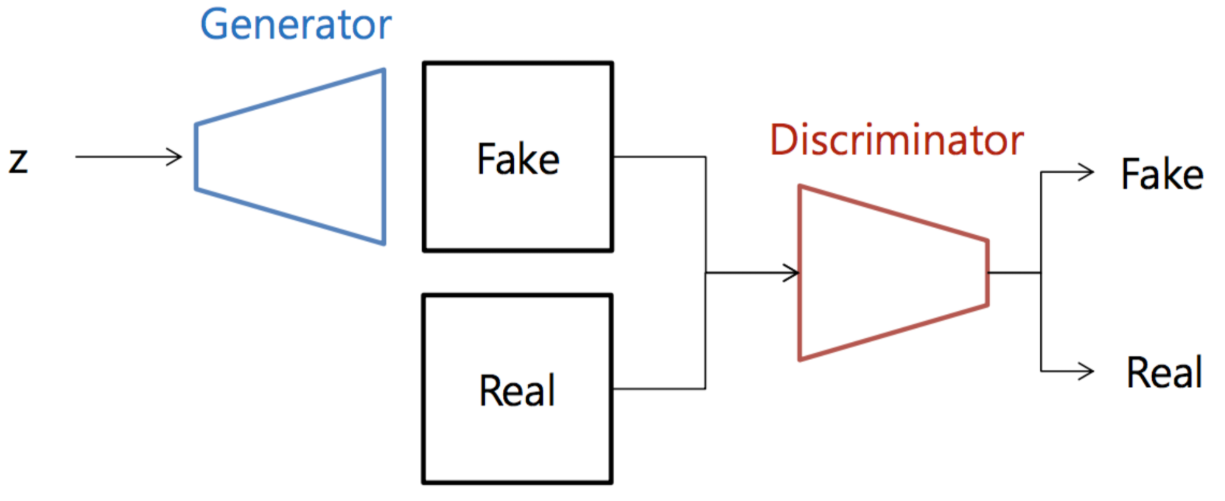
GAN(Generative Adversarial Networks)이라는 이름은 실제 데이터의 분포와 유사한 분포(“Generative” model)를 추정(Estimate)하기 위해 D(Discriminator)와 G(Generator)라는 두 모델을 적대적인(“Adversarial”) 방식을 통하여 모델을 Training시키기 때문에 붙여진 이름이다.

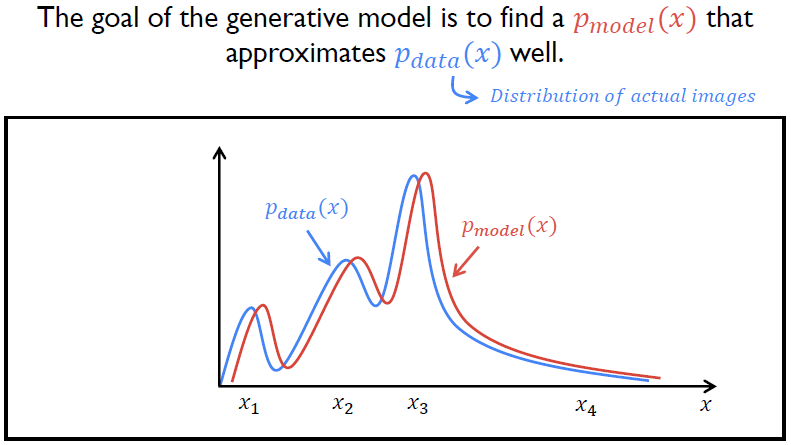
GAN의 최종적인 목적은 Training data과 비교하였을 때 구분할 수 없을 정도로 유사한 가짜 데이터를 생성해낼 수 있도록 Training data의 분포 $P_{data}(x)$를 추정하는 가짜 데이터의 분포 $P_{model}(x)$를 찾는 것이다.

Structure

GAN의 경우 두 개의 네트워크가 사용되어 조금은 복잡한 구조로 학습이 이루어지기 때문에, 글로만 쓰여진 설명을 읽으면 Forward propagation조차 이해가 잘 되지 않을 수 있다. 우선 그림을 통해 결과 값을 어떻게 계산하는지부터 차근차근 살펴보도록 하자.

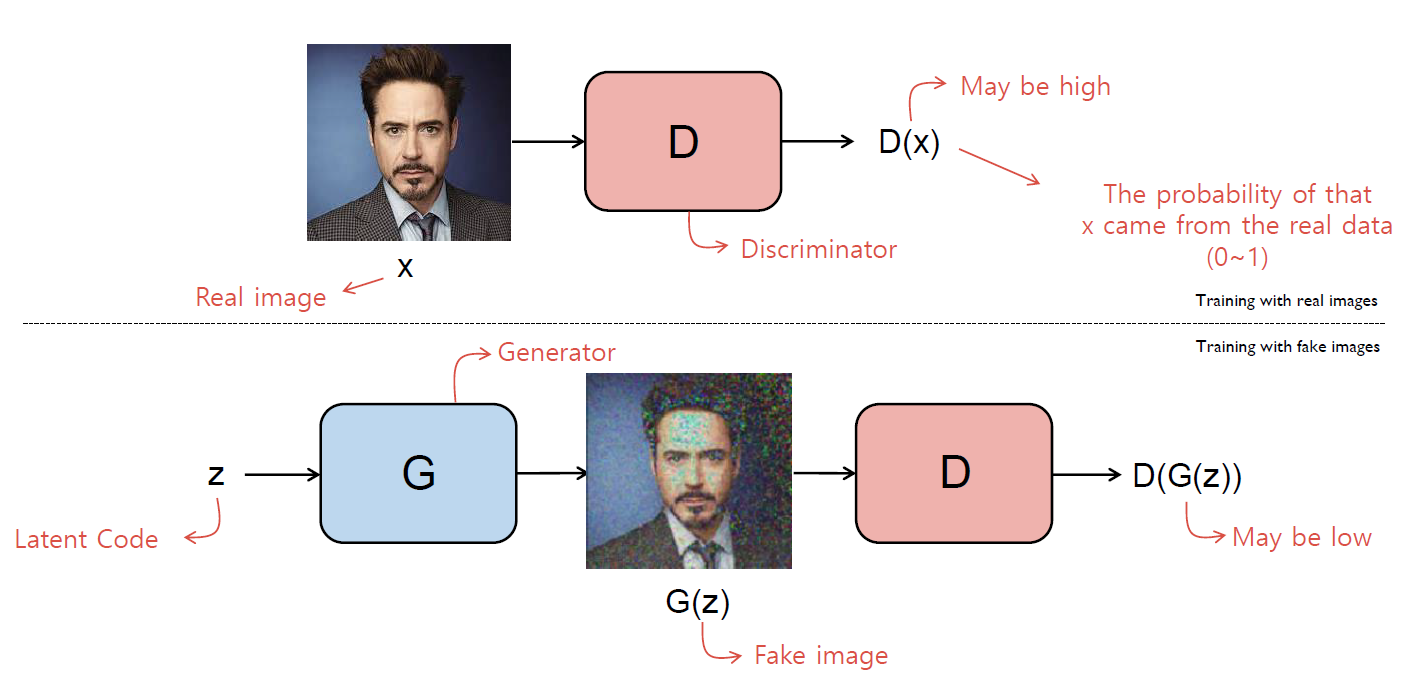
우선 D(Discriminator)부터 살펴보자. D의 역할은 주어진 input이 real data인지 구별하는 것이다. Data $x$가 input으로 주어졌을 때, D의 output $D(x)$는 $x$가 real data일 확률 을 return한다.

G(Generator)의 역할은 D(Discriminator)가 진짜인지 구별할 수 없을 만큼 진짜같은 Fake data를 만들어내는 것이다. 위 그림에서와 같이 난수 vector(Latent Code)가 주어졌을 때 $G$를 통하여 Fake image $G(z)$를 생성 한다. 그러한 $G(z)$를 다시 $D$의 input으로 주면 $D(G(z))$는 $G(z)$가 real data일 확률을 return하게 된다.

D를 학습시킬 때에는 G를 고정시킨 채 실제 데이터($x \sim p_{data}(x)$)가 주어졌을 때에 높은 확률을 return하고, 가짜 데이터($z \sim p_z(z))$)는 낮은 확률을 return해주는 방향으로 weight을 update한다. 진짜 데이터를 잘 가려내는 것이 목표이기 때문이다.

G의 경우 우선 Noise vector $z$를 표준정규분포로부터 sampling한 후에, $z$를 input으로 사용하여 가짜 데이터 $G(z)$를 만든다. 그리고 앞서 학습시킨 D에 $G(z)$를 input으로 주었을 때, 높은 확률을 return해주는 방향으로 weight을 update한다. 가짜 데이터이지만, 마치 실제 데이터인 것처럼 진짜스러운 데이터를 만드는 것이 목표이기 때문이다.

GAN은 이러한 방식으로 G와 D를 번갈아가며 학습시키면서 G 는 D가 구별할 수 없을 만큼 가짜 데이터를 잘 만들 수 있도록, 그리고 D 는 G가 어떠한 가짜 데이터를 만들어내더라도 잘 구별해낼 수 있도록 학습시키면서 균형점을 찾아가도록 만든다.

Objective function

GAN의 목적함수는 다음과 같다.

GAN의 경우 학습해야 하는 네트워크가 2개이며, 서로 충돌되는 학습이 이루어지기 때문에 optimization 또한 따로 이루어지며, 두 가지 optimization $\max_ { D } V\left( D,G \right)$와 $\min_ { G } V\left( D,G \right)$가 순차적으로 이루어진다. $D$와 $G$의 입장에서 하나 씩 살펴보도록 하자.

Objective function of $D$

$D$의 경우, $V(D,G)$를 $D$에 대하여 Maximize하는 방향으로 weight을 update하게 된다. 왜 $V(D,G)$를 $D$에 대하여 Maximize 하는 것인지는 차근차근 살펴보도록 하자.

우선 어떤 $D$가 이상적인 $D$의 모습인지에 대하여 생각해보자. 이상적인 $D$는 진짜 데이터가 input으로 들어왔을 때 1에 가까운 값을 return해야 한다. $D(x_{real})$의 값은 1에 가까워야 하며, 바꿔 말하면 $logD(x_{real})$의 값이 0에 가까워야 한다.

$D(x)$의 경우 $x$가 진짜 데이터일 확률이므로, 0에서 1 사이의 값을 가진다. 즉, $logD(x_{real})$의 값은 $-\infty$에서 0사이의 값을 가지므로, $logD(x_{real})$의 값이 0에 가깝게 만든다는 것은 $logD(x_{real})$의 값을 Maximize시키는 것과 같은 의미임을 알 수 있다.

반면, latent code $z$가 주어지고,$(z \sim p_z(z))$ 이로부터 가짜 데이터 $G(z)$가 생성되었다고 하자. 이 가짜 데이터 $G(z)$를 $D$의 input으로 준다면, $D(G(z))$의 값은 0에 가까워야 하며, 이는 곧 $1-D(G(z))$는 1에 가까워야 한다는 것을 의미한다. 즉, 이상적인 $G$의 경우 $log(1-D(G(z)))$가 0에 가까워야 한다.

이는 $1-D(G(z))$의 값을 Maximize하는 것과 같고, 바꿔말하면 $log(1-D(G(z)))$를 Maximize하는 것과도 같다.

즉, 위 두가지를 종합하여 진짜를 진짜로, 가짜를 가짜로 잘 구분하는 $D$를 만들기 위해서는 $V(D,G)$를 $D$에 대하여 Maximize해야 한다.

Objective function of $G$

$G$의 경우, $V(D,G)$를 $G$에 대하여 Minimize 하는 방향으로 weight을 update하게 된다.

단, $G$에 대한 목적 함수에서는 진짜 데이터가 들어오는 경우를 고려할 필요가 없으므로, 목적함수를 위와 같이 바꿔 생각할 수 있다.

이제 $V(G)$를 $G$에 대하여 왜 Minimize 하는 것인지에 대하여 살펴보도록 하자.

반면, latent code $z$가 주어지고,$(z \sim p_z(z))$ 이로부터 가짜 데이터 $G(z)$가 생성되었다고 하자. $G$의 입장에서는 이 가짜 데이터 $G(z)$를 $D$의 input으로 주었을 때, $D$가 진짜 데이터로 오인할만큼 진짜같아야 하므로, $D(G(z))$의 값은 1에 가깝도록 $G(z)$를 생성해야 한다. 이는 $1-D(G(z))$의 값을 Minimize하는 것과 같고, 바꿔말하면 $log(1-D(G(z)))$를 Minimize하는 것과도 같다.

Heuristic Objective function of $G$

$G$의 objective function의 경우, 위에서 살펴보았듯이 다음을 minimize시키는 것이다.

하지만 이는 Practical한 입장에서 GAN을 training시킬 때 좋지 않은 방법이다. 다음 그림을 살펴보도록 하자.

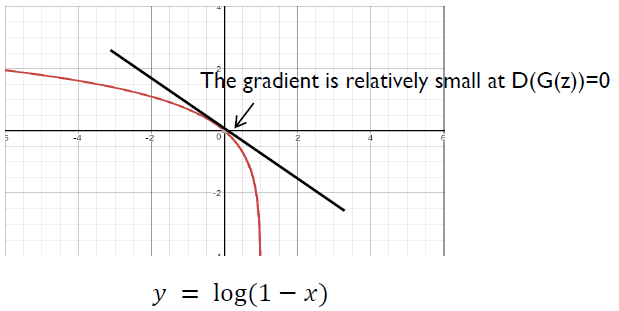
$log(1-x)$ 함수의 그래프이다. 우리는 GAN의 학습 초기에 $G$의 성능이 좋지 않아, $D(G(z))$의 값이 0에 가까운 값이 나올 것이라는 것을 예상할 수 있다. 즉, 초기 학습 과정에서 $log(1-x)$ 함수 상의 $x=0$ 근방에서 gradient를 구하여 weight을 update하게 되는데, 그림에서 볼 수 있듯이 해당 영역에서는 Gradient가 매우 작은 것을 확인할 수 있다. 즉, 학습이 매우 더디게 이루어질 것이라는 것을 알 수 있다.

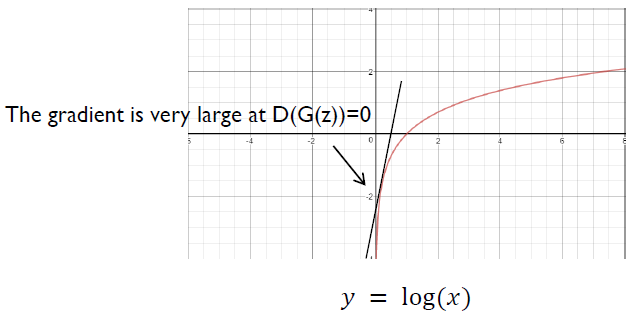
반면, $log(x)$ 함수의 경우는 이야기가 다르다. $log(x)$ 함수의 경우 $x=0$ 근방에서의 gradient가 매우 커서 학습 초기에 training이 매우 잘 될 것이라는 것을 유추할 수 있다. 또한, 학습이 진행됨에 따라 $G$가 가짜 데이터를 잘 만들 수 있도록 학습될 것이고, 이에 따라 $D(G(z))$의 값이 점점 더 1에 가까워지게 될 것이다. $log(x)$ 함수를 보면 $x=0$ 근방에서는 Gradient가 매우 크다가 $x=1$에 가까워 질수록 Gradient가 점점 줄어든다는 것을 확인할 수 있다.

즉, $G$의 목적함수를 다음과 같이 $log(x)$로 나타낸 함수로 바꾸면 초기에는 학습 속도를 높이고, 후기에는 학습 속도를 조절하여 줄일 수 있게 되어 매우 효율적인 학습이 가능하다. 이러한 이유로 실제 모델에서는 다음과 같은 목적함수를 사용한다. 상당히 Heuristic한 방법이지만 Ian Goodfellow의 논문에서 실제로 나오는 내용으로써, 실제로 모델을 짤때도 이 목적함수를 사용하게 된다.

Why does GANs work?

GAN이 Practical하게 잘 작동하는 것은 이미 잘 알려진 사실이다. 하지만 GAN의 목적함수를 optimize하는 것이 어떻게 가짜 데이터가 진짜 데이터와 같이 생성될 수 있도록 하는 것인지에 대하여 조금 생각해볼 필요가 있다.

이에 대하여 Ian Goodfellow의 원 논문 Generative Adversarial Networks에 증명되어 있는 내용을 간단하게 정리하면 다음과 같다.

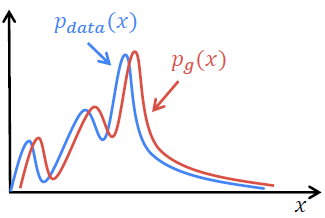
즉, GAN에서 $\min_ { G }\max_ { D }{ V\left( D,G \right)}$ 문제를 푸는 것은 진짜 데이터의 분포 $p_{data}$와 가짜 데이터의 분포 $p_{q}$간의 Jenson-Shannon divergence 를 minimize하는 것과 같기 때문에 GAN이 잘 작동하는 것임을 알 수 있다.

Source code: MNIST dataset

상당히 깔끔하게 구현해 놓은 github이 있어 여기를 참고하여 직접 구현해 보았다.

import os
import torch
import torchvision

# setting device
device = 'cuda' if torch.cuda.is_available() else 'cpu'

# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)

# parameters
learning_rate_D = 0.0002
learning_rate_G = 0.0002
latent_size = 64
hidden_size = 256
image_size = 784
n_epochs = 200
batch_size = 100
dataset_dir = '../../data/'
sample_dir = 'samples'

# creating directory of output samples
if not os.path.exists(sample_dir):
    os.makedirs(sample_dir)

# dataset for MNIST
transform = torchvision.transforms.Compose([
    torchvision.transforms.ToTensor(),
    torchvision.transforms.Normalize([0.5], [0.5])])

mnist = torchvision.datasets.MNIST(root=dataset_dir,
                                   train=True,
                                   transform=transform,
                                   download=True)

# data loader
data_loader = torch.utils.data.DataLoader(dataset=mnist,
                                          batch_size=batch_size,
                                          shuffle=True)

# GAN
# D(Discriminator)
D = torch.nn.Sequential(
        torch.nn.Linear(image_size, hidden_size),
        torch.nn.LeakyReLU(0.2),
        torch.nn.Linear(hidden_size, hidden_size),
        torch.nn.LeakyReLU(0.2),
        torch.nn.Linear(hidden_size, 1),
        torch.nn.Sigmoid()
).to(device)

# G(Generator)
G = torch.nn.Sequential(
        torch.nn.Linear(latent_size, hidden_size),
        torch.nn.ReLU(),
        torch.nn.Linear(hidden_size, hidden_size),
        torch.nn.ReLU(),
        torch.nn.Linear(hidden_size, image_size),
        torch.nn.Tanh()
).to(device)

# loss
criterion = torch.nn.BCELoss()

# optimizer
D_optimizer = torch.optim.Adam(D.parameters(), lr = learning_rate_D)
G_optimizer = torch.optim.Adam(G.parameters(), lr = learning_rate_G)

# Training
n_steps = len(data_loader)
ones = torch.ones(batch_size, 1).to(device)
zeros = torch.zeros(batch_size, 1).to(device)
for epoch in range(n_epochs):
    for i, (images, _) in enumerate(data_loader):
        ### input
        X = images.reshape(batch_size, -1).to(device)

        #############################################
        ###  Trainig D(Discriminator)    
        #############################################
        # D
        D_X = D(X)
        D_loss_real = criterion(D_X, ones)
        # G
        z = torch.randn(batch_size, latent_size).to(device)
        G_z = G(z)
        D_G_z = D(G_z)
        D_loss_fake = criterion(D_G_z, zeros)
        # optimization
        D_loss = D_loss_real + D_loss_fake
        D_optimizer.zero_grad() # reset gradients of D optimizer
        D_loss.backward()       # back propagation
        D_optimizer.step()      # updating weights

        #############################################
        ###  Training G(Generator)    
        #############################################
        z = torch.randn(batch_size, latent_size).to(device)
        G_z = G(z)
        D_G_z = D(G_z)
        # optimization
        G_loss = criterion(D_G_z, ones)
        G_optimizer.zero_grad() # reset gradients of G optimizer
        G_loss.backward()       # back propagation
        G_optimizer.step()      # updating weights

        #############################################
        ###  print
        #############################################
        if (i+1) % 300 == 0:
            print('Epoch: [{}/{}], Step: [{}/{}], D_loss: {:.4f}, G_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'
                  .format(epoch+1, n_epochs, i+1, n_steps, D_loss.item(), G_loss.item(), D_X.mean().item(), D_G_z.mean().item())
            )


    #############################################
    ###  sample images
    #############################################    
    # saving real images
    if epoch == 0:
        images = X.reshape(X.size(0), 1, 28, 28)
        images_denormed = ((images+1)/2).clamp(0,1)
        name_save = os.path.join(sample_dir, 'real.png')
        torchvision.utils.save_image(images_denormed, name_save)
    else:
        pass
    # saving fake images
    images = G_z.reshape(D_G_z.size(0), 1, 28, 28)
    images_denormed = ((images+1)/2).clamp(0,1)
    name_save = os.path.join(sample_dir, 'fake_{}.png'.format(epoch))
    torchvision.utils.save_image(images_denormed, name_save)

Training이 진행되면서 실제 데이터와 유사한 데이터를 생성해내는 것을 확인할 수 있다.

Reference

Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio(2014). Generative Adversarial Networks. Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680.

고려대학교 최윤제 연구원님의 Naver D2(Naver Engineering) 발표자료

ratsgo’s blog, Generative Adversarial Network