프로그래머스(Algorithm)-완주하지 못한 선수(Hash)

문제

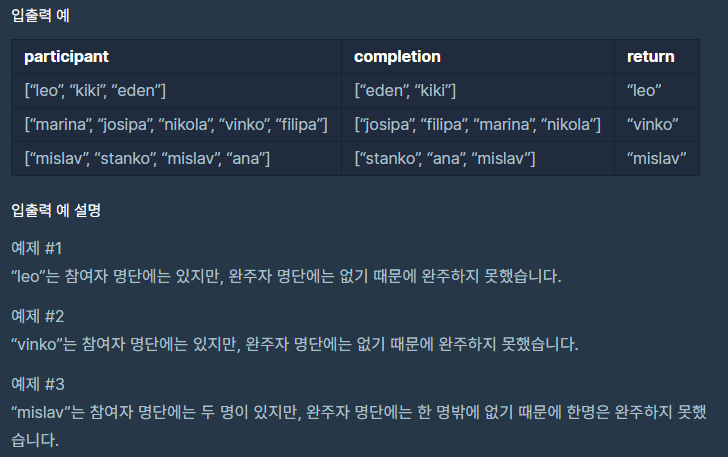
이해

주목해야 할 부분은 동명이인이 있을 수 있다는 점이다.(동명이인이 없다면 문제는 매우 쉽다. set으로 생각하여 차집합을 구해주면 된다.) 하지만 동명이인이 있기 때문에 이 경우 다른 접근 방식이 필요하다.

구체적으로는, 이름에 대해서 몇 번이나 배열에 등장했는지 숫자를 저장하는 구조가 필요 필요하다.

만약 숫자(인덱스)가 주어지고, 그 숫자(인덱스)에 해당하는 이름이 무엇인지 알고싶은 경우라면 선형 배열(Linear Array)를 사용할 수 있다.

반대로 이 문제와 같이 이름이 주어지면 그 이름에 해당하는 숫자(인덱스)를 찾고 싶은 경우에는 해시(Hash)를 사용할 수 있다.

해시(Hash)

자료구조 시간에 배웠던 해시(Hash)를 다시 한 번 복습해보자.

이 문제에서는 사람의 이름이 key가 되고, key들이 Hash Table의 어느 위치에 있을지를 정하여 Hash Table 안에 값들을 저장(Mapping)한다.

이렇게 이름을 key로 하고, 서로 다른 칸의 값과 mapping되도록 구조를 짜는 것을 Hash 라고 한다. 그리고 그러한 mapping을 hash function이라고 부른다.

Hash Table의 각각의 칸들은 해시 버킷(Hash Bucket)이라고 부른다. 해시 버킷의 수가 많을 수록 서로 다른 키가 서로 다른 버킷에 mapping될 가능성이 높아질 것이다. Hash function또한 Hash Bucket의 총 개수에 맞 구성되어야 한다.

항상 모든 key가 다른 값에 mapping되는 것을 보장할 수는 없지만, 가급적이면 다른 값에 mapping되도록 한다. 물론 같은 값에 mapping될 수도 있는데, 이러한 상황을 해시 충돌(collision)이라고 한다. 이러한 문제가 발생할 경우, 같은 값에 대한 다른 칸을 만들고, 그 칸들이 어떤 키와 연결되는지 명시하는 방법을 통해 해결할 수 있다.

파이썬에는 사전(Dictionary)를 구현할 때 내부적으로 해시 테이블을 이용하기 때문에 Dictionary를 활용하여 문제를 풀 수 있을 것이다. Dictionary를 활용할 경우, Dictionary의 원소들을 해시를 이용하여 상수시간(O(1))에 접근 가능하다는 특징이 있다.

풀이

이 문제를 Hash를 이용해 푸는 방법은 다음과 같다.

def solution(participant, completion):
    d = {}
    for x in participant:
        d[x] = d.get(x,0)+1
    for x in completion:
        d[x] -= 1
    dnf = []
    for k, v in d.items():
        if v>0:
            dnf.append(k)
    answer = dnf[0]     
    return answer

list comprehension을 활용한다면 다음과 같이 더 간단하게 짤수도 있다.

def solution(participant, completion):
    d = {}
    for x in participant:
        d[x] = d.get(x,0)+1
    for x in completion:
        d[x] -= 1
    dnf = [k for k, v in d.items() if v > 0]
    answer = dnf[0]
    return answer

for문이 두 개가 들어가있다. 첫 번째 for문(3~4행)에서는 participant라는 배열의 길이 N에 비례하는 복잡도를 가지며, 두 번째 for문(5~6행) 또한 N에 비례하는 복잡도를 가진다. 7행에서는 if의 조건이 만족되는 경우 원소들을 골라서 리스트를 만들어내는 연산이다. 이 경우, 사전에 있는 모든 원소들을 꺼내야 하기 때문에 사전의 크기에 비례한다. 그런데 그 사전 d의 크기 또한 participant의 크기에 비례하므로, N에 비례하는 시간 복잡도를 가지는 것을 알 수 있다. 따라서 이 함수 전체의 시간 복잡도는 인자로 주어진 participant라는 배열의 길이 N에 비례하는 O(n) 인 것을 알 수 있다.

이렇게 Linear time 알고리즘(O(n))을 만들 수 있었던 이유는 사전(Dictionary)은 내부적으로 해시(Hash)를 통해 구현되고, 해시 테이블이 키를 기준으로 상수 시간에 접근할 수 (읽고 쓸 수) 있었기 때문에(O(1)) 가능한 것이다.

다른 풀이 방법

사실 다음과 같이 sorting을 이용하는 방법 또한 가능하다.

def solution(participant, completion):
    participant.sort()
    completion.sort()
    for i in range(len(completion)):
        if participant[i] != completion[i]:
            return participant[i]
    return participant[-1]

해시가 O(n) 의 시간 복잡도를 가지는 것에 비하여, 정렬은 최적의 경우 O(nlogn) 의 시간 복잡도를 가진다. 따라서 이 문제의 경우 sorting보다는 Hash를 이용하여 푸는 것이 본래 문제의 의도에 가깝다고 볼 수 있다.

Reference

https://hsin.hr/coci/archive/2014_2015/contest2_tasks.pdf