프로그래머스(Algorithm)-가장 큰 수(Sort)

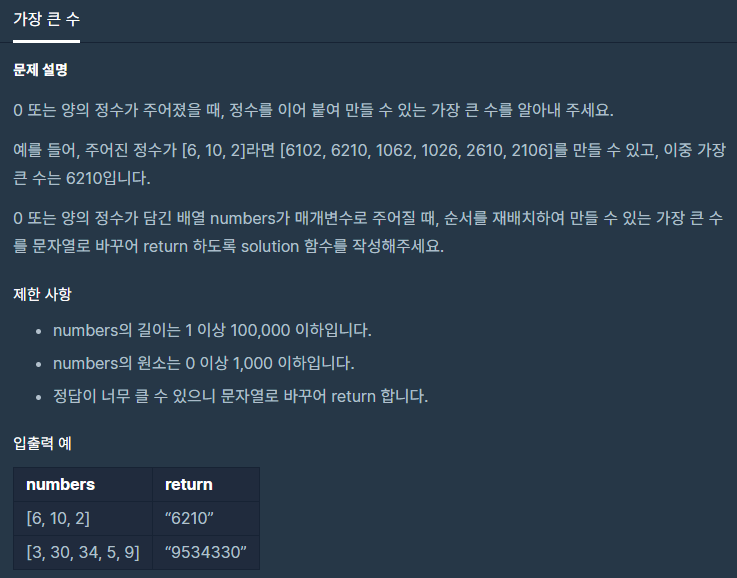
문제

이해

이 문제를 보았을 때 가장 먼저 드는 생각은 단계에 따라 후보를 순서대로 하나씩 살펴보면서 꺼내서 오른쪽에 붙여가면 되겠다는 생각이다. 예를들면 다음과 같다.

[3, 30, 34, 5, 9] 에서 9를 선택하여 9를 만들고,
[3, 30, 34, 5] 에서 5를 선택하여 95를 만들고,
[3, 30, 34] 에서 34를 선택하여 9534를 만들고,
[3, 30] 에서 3을 선택하여 95343를 만들고,
[30] 에서 30을 선택하여 9534330를 만들고,
[] 와 같이 남은 숫자가 없으므로 큰 수 만들기를 종료한다.

하지만 이렇게 알고리즘을 짤 경우 시간복잡도 O(n^2) 의 알고리즘이 되므로 효율적이지 않다.(각 단계에서 일일이 살펴보므로 $n$번, 단계가 $n$번이므로 총 $n^2$.)

이 문제를 효율적으로 풀기 위해서는 Sorting하는 것이 핵심이다. n번의 단계에서 일일이 살펴보는 것이 아닌($n$), 목적에 맞게 sort하여 선택하면 $nlog(n)$의 시간복잡도를 가지게 된다. 따라서 sort를 활용할 경우, 시간복잡도 O(nlog(n)) 의 알고리즘을 만들 수 있다.

단, 여기서 sort하는 기준이 오름차순/내림차순이 아닌, 결과를 최선으로 만드는 순서라는 것임을 유념해야 한다.

예를들어 다음과 같은 숫자가 남았다고 생각해보자.

[34, 342, 343, 344]

이 때 가장 최적의 수를 어떻게 찾을 수 있을까? 이 문제의 핵심은 만약 어떠한 상황에서 특정 숫자가 최적의 숫자라면, 그 상황에서 가능한 가장 큰 수는 그 특정 숫자가 반복되는 숫자 라는 것이다.

예를들어 34와 344를 비교해보자.

만약 34가 최적의 숫자가 맞다면, 그 상황에서 만들어질 수 있는 이론상 가장 큰 숫자는 343434…34가 된다.

만약 344가 최적의 숫자가 맞다면, 그 상황에서 만들어질 수 있는 이론상 가장 큰 숫자는 344344344…344가 된다.

“numbers의 원소는 0 이상 1,000 이하입니다.”라는 조건을 반영하여, 4번째 자리에서 끊어 가장 최적의 경우를 만들어낼 수 있는 숫자를 찾아본다. 즉, 예시에서 3434와 3443을 비교했을 때 3443이 더 크므로, 34와 344 중에서는 344가 최적의 숫자가 된다.

또한, input이 0들로 이루어져있는 경우에 대하여 예외처리하는 것또한 잊지 않도록 한다.

풀이

def solution(numbers):

    numbersStr = [str(x) for x in numbers]
    l = sorted(numbersStr, key=lambda x:(x*4)[:4], reverse=True)

    if l[0] == '0':
        answer = '0'
    else:
        answer = ''.join(l)

    return answer

Reference

https://programmers.co.kr/learn/courses/30/lessons/42746