우선, 해당 포스트는 Stanford University School of Engineering의 CS231n 강의자료와 모두를 위한 딥러닝 시즌2의 자료를 기본으로 하여 정리한 내용임을 밝힙니다.
Covariate Shift
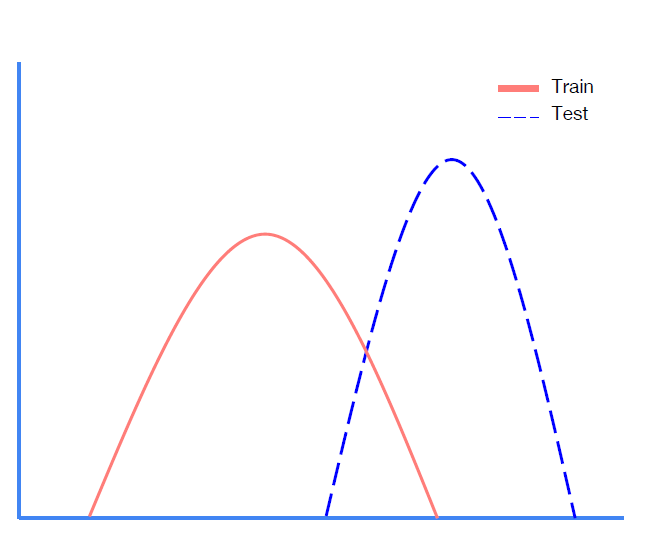
이는 또한 Training set($X_{train}$)의 분포와 Test set($X_{test}$)의 분포의 차이가 있는 경우, 이를 Covariate Shift 라고 부른다.
Covariate Shift는 모델의 성능 저하에 큰 영향을 미친다. 그 이유를 직관적으로 잘 설명해주는 자료가 있어 JUNSIK HWANG님의 블로그에서 아래 그림을 가지고 왔다.
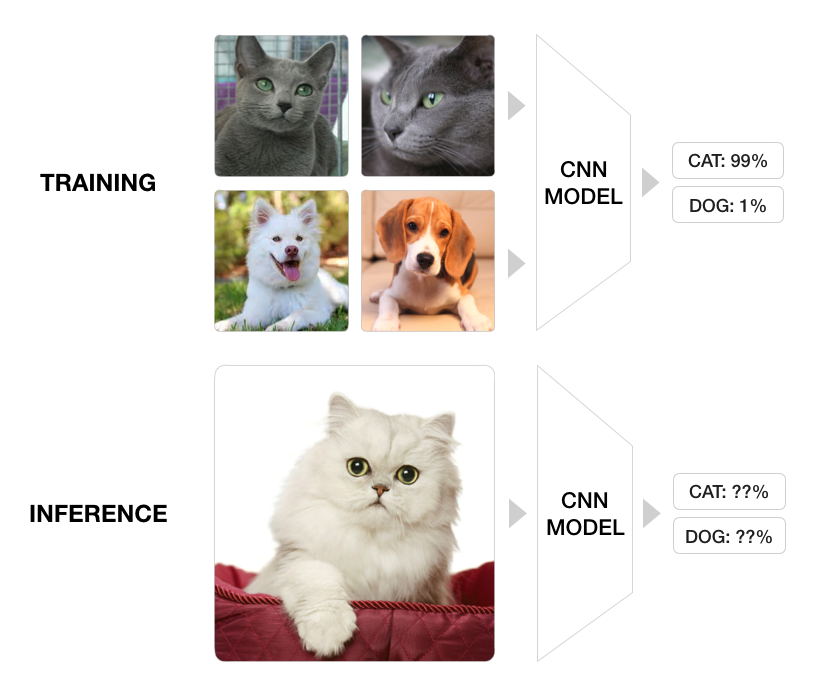
고양이와 강아지를 분류하는 문제를 풀고있으며, Training dataset에는 러시안 블루 고양이만 있고, Test dataset에는 페르시안 고양이만 있다고 하자.(즉, Covariate Shift를 일부러 만들어보자.)
이 때 Training data의 러시안 블루 고양이에 대한 우리가 적합시킨 모델의 분류 정확도(Training Accuracy)는 99%에 달한다.
하지만 Test dataset에는 페르시안 고양이만 있는 상황이다. 이 때 우리가 train시킨 모델에 이러한 Test dataset을 적용하면 어떤 결과가 발생할까?
페르시안 고양이의 털 색깔(흰색)을 보고 “Training set에서는 회색 털을 가지고 있어야 고양이라고 배웠는데, Testset의 이 친구는 하얀색 털을 가지고 있구나. 그럼 이 친구는 강아지 일 수도 있겠다.” 라는 판단을 할 수 있게 되고, 결과적으로 오분류의 가능성이 높아진다.
즉, Training dataset과 Input dataset의 분포에 대한 차이는 모델의 성능 저하에 큰 영향을 미칠 수 있는 것이다.
Internal Covariate Shift
Training/Test dataset 간의 차이에 대한 문제(Covariate Shift)를 각 Mini Batch 간 input 데이터의 차이에 의한 문제로 확장 시킨 것을 Internal Covariate Shift 라고 한다.
Neural Networks에서 모든 Training data를 한 번에 사용하지 않고 Mini batch를 사용할 경우, 각 step에서 사용되는 Training data는 매번 달라지게 된다. 이렇게 배치 간의 데이터 분포가 다른 경우를 Internal Covariate Shift 라고 한다.
이러한 Internal Covariate Shift 문제는 Layer의 수가 많으면 더욱 더 큰 문제가 된다.
일반적인 Neural Networks에서는 여러 layers를 사용하며, 각 layer마다 input을 받아 linear combination을 구한 후 Activation function을 적용하여 output을 구해주는 작업이 이루어 진다.
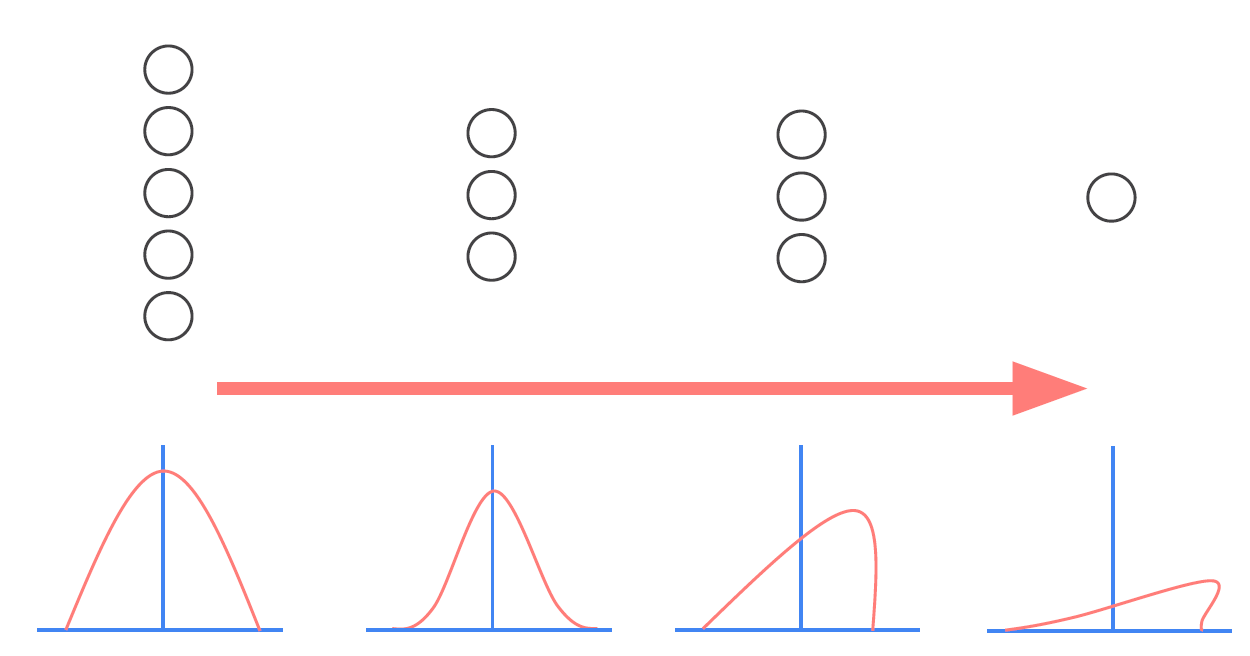
결과적으로 이 때문에 각 layer의 input data $x$의 분포(Distribution)가 달라지게 되며, 뒷단에 위치한 layer일 수록 변형이 누적되어 input data의 분포는 상당히 많이 달라지게 된다.
이런 상황이 발생할 경우, 모델의 parameter들이 일관적인 학습을 하기가 어려워진다.
Batch Normalization
이러한 Internal Covariate Shift문제를 해결하기 위하여 고안된 아이디어가 바로 Batch Normalization 이다.
Batch Normalization은 loffe and Szegedy(2015)에 의하여 제안된 개념이며, 논문에서 제시된 방법은 다음과 같다.

이제 한 단계 한 단계씩 자세히 살펴보도록 하자.
Batch Normalization while Training
$K$개의 Mini batch $\text{mini-batch}_{k},\;\;k=1,2,\cdots,K$가 존재한다고 가정하자.
각 Mini batch마다 $m$개(batch size)의 데이터 $x_1,x_2,\cdots,x_m$이 존재한다.
\[B = \left \lbrace x_1,\cdots, x_m \right \rbrace\]우리는 각 Mini batch에 들어가 있는 $x_1,\cdots,x_m$에 대하여 표본 평균 $\mu_B = {\frac 1 m}\sum_{i=1}^m x_i$과 표본 분산 $\sigma_B^2 = {\frac 1 m} \sum_{i=1}^m (x_i-\mu_B)^2$을 구할 수 있다.
이 값들을 활용하여 다음과 같이 input data $x_1,\cdots,x_m$을 normalize해줄 수 있다.
\[\hat x_i = {\frac {x_i-\mu_B} {\sqrt{\sigma_B^2+\epsilon}}}\]한 Batch 내의 표본평균과 표본표준편차를 사용하여 normalize해주는 것에서 끝나지 않고, $\gamma$와 $\beta$라는 parameter를 활용하여 scale and shift시켜준다.
\[y_i = \gamma \hat x_i + \beta\]scale and shift는 normalize를 다시 어느정도 풀어주는 작업이라고 볼 수 있다. 모수 $\gamma$와 $\beta$ 또한 training 과정에서 학습시켜야 하는 parameter이다.
Batch Normalization while Testing
Test data에 대해서도 역시 Batch Normalization을 취해준다. 하지만 그 방식은 Training 때와는 조금 다르다.
만약 Training 때와 같은 방식으로 Test 때 Normalize시켜준다면 한 가지 문제점이 발생한다. 다음 상황을 생각해보자.
Batch-size가 8이며, 어떠한 두 Minibatch $B_1$과 $B_2$가 다음과 같은 데이터로 구성되어 있다고 하자.
\[\begin{align*} B_1 &= \left \lbrace x_1,x_2,\cdots,x_6,x_7,x_8 \right \rbrace\\ B_2 &= \left \lbrace x_1,x_2,\cdots,x_6,x_9,x_{10} \right \rbrace \end{align*}\]이때 Minibatch_1의 표본평균과 표본분산 $\mu_1, \sigma_1^2$은 Minibatch_2의 표본평균과 표본분산 $\mu_2, \sigma_2^2$과 분명 다를 것이다.
이 때문에 같은 Test data $x_1$의 normalization 결과가 minibatch_1과 minibatch_2에서 달라지게 된다.
이를 방지하기 위하여 Test set에서의 Batch Normalization은 조금 다르게 이루어진다.
해당 Mini Batch의 표본평균과 표본분산을 쓰는것이 아닌, Training 과정의 $K$개의 Mini Batch에서 얻은 $K$개의 표본평균을 평균낸 값(Learning mean)과, $K$개의 표본분산을 평균낸 값(Learning variance)을 대신 사용한다.
Example
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
import matplotlib.pylab as plt
# setting device
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# for reproducibility
torch.manual_seed(1)
if device == 'cuda':
torch.cuda.manual_seed_all(1)
# parameters
learning_rate = 0.01
training_epochs = 10
batch_size = 32
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)
# dataset loader
train_loader = torch.utils.data.DataLoader(dataset=mnist_train,
batch_size=batch_size,
shuffle=True,
drop_last=True)
test_loader = torch.utils.data.DataLoader(dataset=mnist_test,
batch_size=batch_size,
shuffle=False,
drop_last=True)
# model
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 32, bias=True)
linear3 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.ReLU()
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)
nn_linear1 = torch.nn.Linear(784, 32, bias=True)
nn_linear2 = torch.nn.Linear(32, 32, bias=True)
nn_linear3 = torch.nn.Linear(32, 10, bias=True)
bn_model = torch.nn.Sequential(linear1, bn1, relu,
linear2, bn2, relu,
linear3).to(device)
nn_model = torch.nn.Sequential(nn_linear1, relu,
nn_linear2, relu,
nn_linear3).to(device)
# define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device) # Softmax is internally computed.
bn_optimizer = torch.optim.Adam(bn_model.parameters(), lr=learning_rate)
nn_optimizer = torch.optim.Adam(nn_model.parameters(), lr=learning_rate)
# Save Losses and Accuracies every epoch
# We are going to plot them later
train_losses = []
train_accs = []
valid_losses = []
valid_accs = []
train_total_batch = len(train_loader)
test_total_batch = len(test_loader)
for epoch in range(training_epochs):
bn_model.train() # set the model to train mode
for X, Y in train_loader:
# reshape input image into [batch_size by 784]
# label is not one-hot encoded
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_optimizer.zero_grad()
bn_prediction = bn_model(X)
bn_loss = criterion(bn_prediction, Y)
bn_loss.backward()
bn_optimizer.step()
nn_optimizer.zero_grad()
nn_prediction = nn_model(X)
nn_loss = criterion(nn_prediction, Y)
nn_loss.backward()
nn_optimizer.step()
with torch.no_grad():
bn_model.eval() # set the model to evaluation mode
# Test the model using train sets
bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
for i, (X, Y) in enumerate(train_loader):
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, nn_loss, bn_acc, nn_acc = bn_loss / train_total_batch, nn_loss / train_total_batch, bn_acc / train_total_batch, nn_acc / train_total_batch
# Save train losses/acc
train_losses.append([bn_loss, nn_loss])
train_accs.append([bn_acc, nn_acc])
print(
'[Epoch %d-TRAIN] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), nn_loss.item(), nn_acc.item()))
# Test the model using test sets
bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
for i, (X, Y) in enumerate(test_loader):
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, nn_loss, bn_acc, nn_acc = bn_loss / test_total_batch, nn_loss / test_total_batch, bn_acc / test_total_batch, nn_acc / test_total_batch
# Save valid losses/acc
valid_losses.append([bn_loss, nn_loss])
valid_accs.append([bn_acc, nn_acc])
print(
'[Epoch %d-VALID] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), nn_loss.item(), nn_acc.item()))
print()
print('Learning finished')
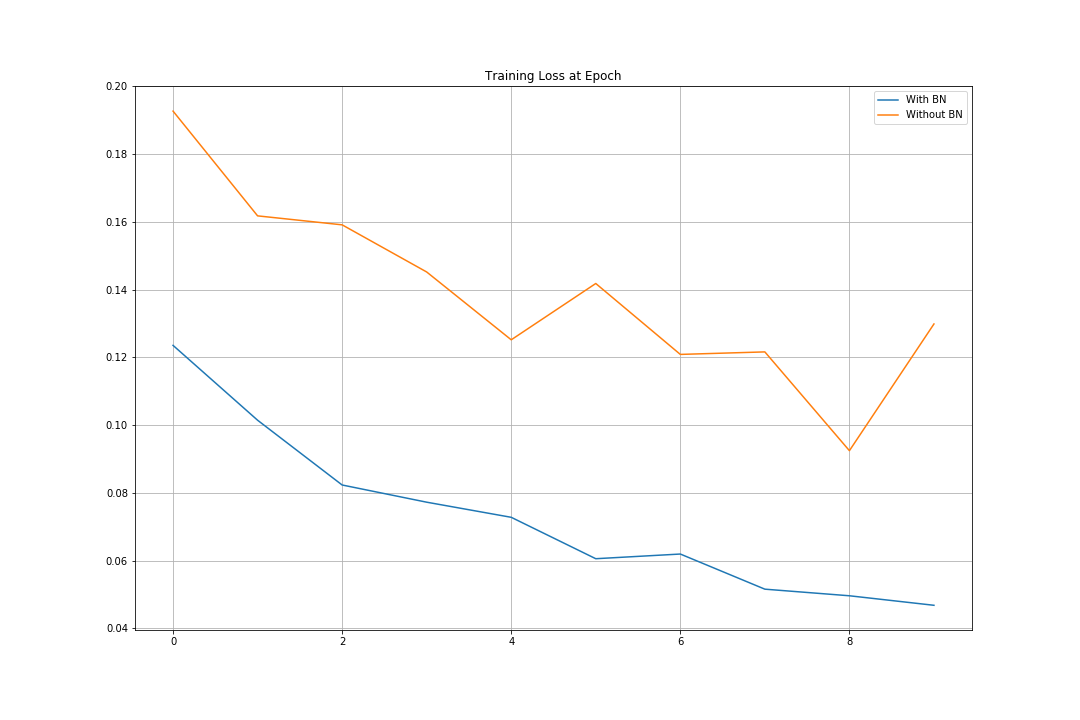
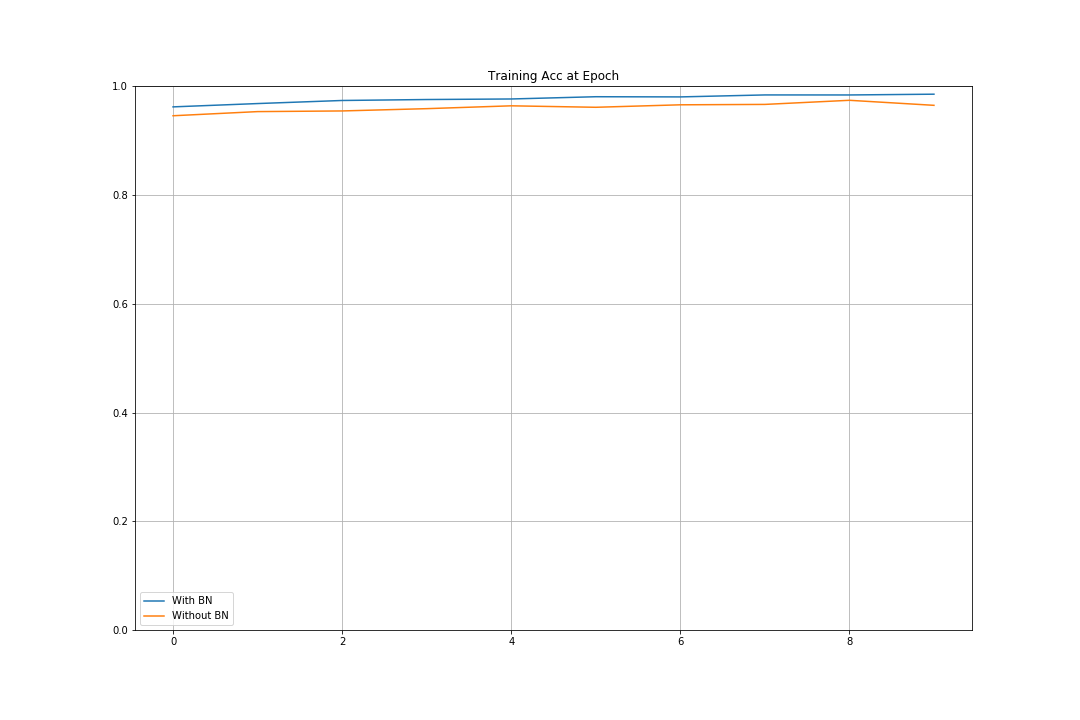
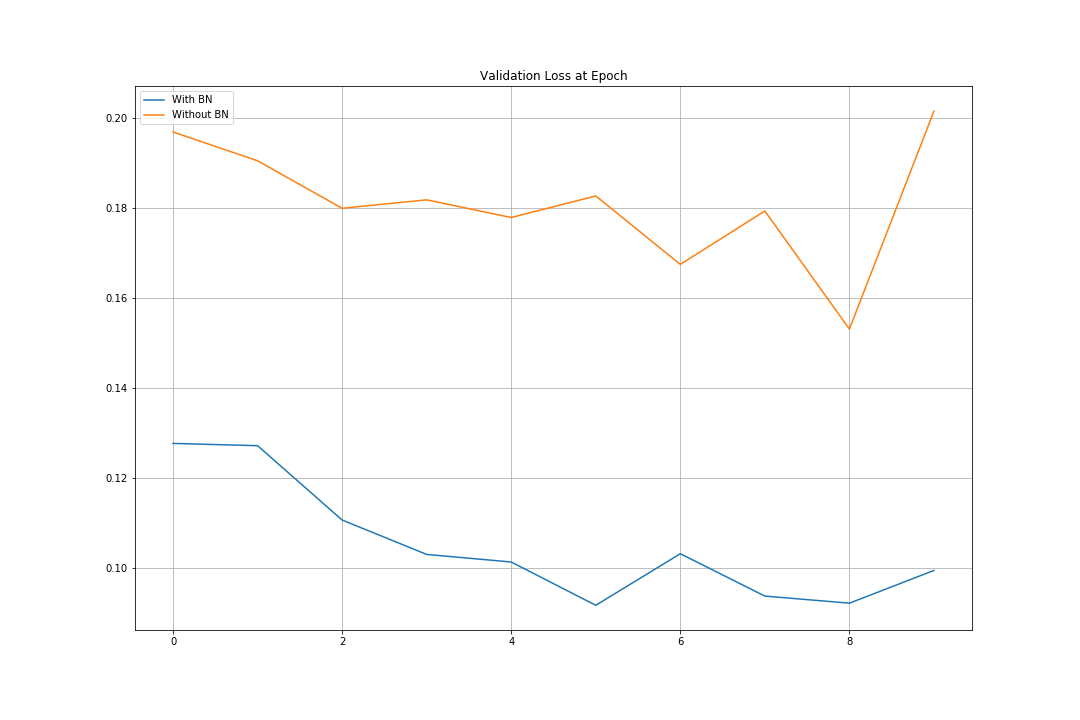
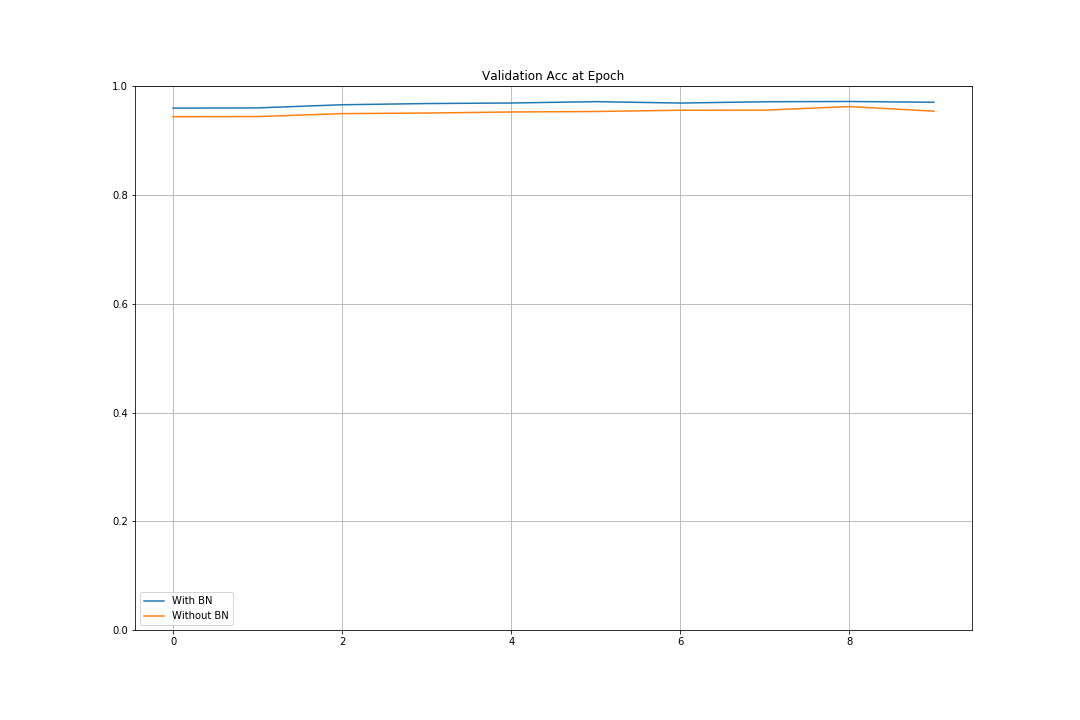
Batch Normalization을 하지 않았을 때의 Accuracy는 95.55%, 해주었을 때의 Accuracy는 97.8%로 더 높게 나타난다.
def plot_compare(loss_list: list, ylim=None, title=None) -> None:
bn = [i[0] for i in loss_list]
nn = [i[1] for i in loss_list]
plt.figure(figsize=(15, 10))
plt.plot(bn, label='With BN')
plt.plot(nn, label='Without BN')
if ylim:
plt.ylim(ylim)
if title:
plt.title(title)
plt.legend()
plt.grid('on')
plt.show()
plot_compare(train_losses, title='Training Loss at Epoch')
plot_compare(train_accs, [0, 1.0], title='Training Acc at Epoch')
plot_compare(valid_losses, title='Validation Loss at Epoch')
plot_compare(valid_accs, [0, 1.0], title='Validation Acc at Epoch')
Reference
CS231n, Stanford University School of Engineering